Question

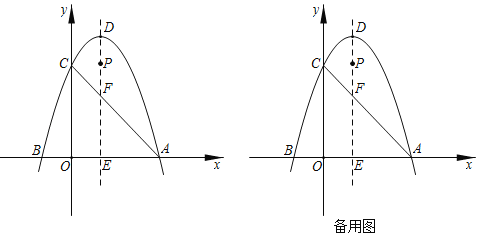
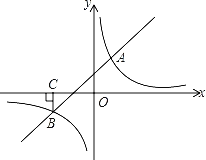
【题目】如图，一次函数y＝kx+b与反比例函数y＝的图象交于A（2，3），B（﹣3，n）两点．

（1）求反比例函数的解析式；

（2）过B点作BC⊥x轴，垂足为C，若P是反比例函数图象上的一点，连接PC，PB，求当△PCB的面积等于5时点P的坐标．

Answer 1

【答案】（1）y＝；（2）点P的坐标为（﹣8，﹣），（2，3）．

【解析】

（1）将A坐标代入反比例函数解析式中求出m的值，即可确定出反比例函数解析式；
（2）由B点（-3，n）在反比例函数y＝的图象上，于是得到B（-3，-2），求得BC=2，设△PBC在BC边上的高为h，根据三角形的面积公式列方程即可得到结论．

（1）∵反比例函数y＝的图象经过点A（2，3），

∴m＝6．

∴反比例函数的解析式是y＝；

（2）∵B点（﹣3，n）在反比例函数y＝的图象上，

∴n＝﹣2，

∴B（﹣3，﹣2），

∴BC＝2，设△PBC在BC边上的高为h，

则BCh＝5，

∴h＝5，

∵P是反比例函数图象上的一点，

∴点P的横坐标为：﹣8或2，

∴点P的坐标为（﹣8，﹣），（2，3）．