题目内容
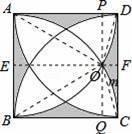
如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积 .


16﹣4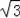
 ﹣
﹣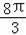
 .
.
【考点】扇形面积的计算;正方形的性质.
【专题】几何图形问题.
【分析】如解答图,作辅助线,利用图形的对称性求解.解题要点是求出弓形OmC的面积.
【解答】解:如图,设点O为弧的一个交点.
连接OA、OB,则△OAB为等边三角形,∴∠OBC=30°.
过点O作EF⊥CD,分别交AB、CD于点E、F,则OE为等边△OAB的高,
∴OE=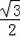
 AB=
AB=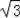
 ,∴OF=2﹣
,∴OF=2﹣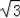
 .
.
过点O作PQ⊥BC,分别交AD、BC于点P、Q,则OQ=1.
S弓形OmC=S扇形OBC﹣S△OBC=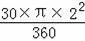
 ﹣
﹣
 ×2×1=
×2×1=
 ﹣1.
﹣1.
∴S阴影=4(S△OCD﹣2S弓形OmC)=4[
 ×2×(2﹣
×2×(2﹣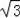
 )﹣2(
)﹣2(
 ﹣1)]=16﹣4
﹣1)]=16﹣4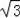
 ﹣
﹣
 .
.
故答案为:16﹣4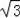
 ﹣
﹣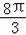
 .
.

【点评】本题考查了扇形的面积公式和正方形性质的+应用,主要考查学生的计算能力,题目比较好,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 B.
B.

