题目内容
 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
(1)求m,k的值;
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:数形结合
分析:(1)根据三角形的面积公式即可求得m的值;
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y=
的图象有两个不同的公共点,则方程
=nx+2有两个不同的解,利用根的判别式即可求解.
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y=
| k |
| x |
| 2 |
| x |
解答:解:(1)由已知得:S△AOB=
×1×m=1,
解得:m=2,
把A(1,2)代入反比例函数解析式得:k=2;
(2)由(1)知反比例函数解析式是y=
,
由题意得:
有两个不同的解,即
=nx+2有两个不同的解,
方程去分母,得:nx2+2x-2=0,
则△=4+8n>0,
解得:n>-
且n≠0.
| 1 |
| 2 |
解得:m=2,
把A(1,2)代入反比例函数解析式得:k=2;
(2)由(1)知反比例函数解析式是y=
| 2 |
| x |
由题意得:
|
| 2 |
| x |
方程去分母,得:nx2+2x-2=0,
则△=4+8n>0,
解得:n>-
| 1 |
| 2 |
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为
如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为
 在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.
在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.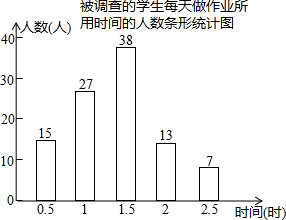 某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案: