题目内容
 把半径为r的圆铁片沿着半径OA、OB剪成面积比为1:2的两个扇形S1、S2(如图),把这两个围成两个无底的圆锥.设这两个圆锥的高分别为h1、h2,则h1与h2的大小比较是
把半径为r的圆铁片沿着半径OA、OB剪成面积比为1:2的两个扇形S1、S2(如图),把这两个围成两个无底的圆锥.设这两个圆锥的高分别为h1、h2,则h1与h2的大小比较是
- A.h1>h2
- B.h1<h2
- C.h1=h2
- D.不能确定
A
分析:利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而利用勾股定理可求得各个圆锥的高,比较即可.
解答:设扇形S2做成圆锥的底面半径为R2,
由题意知,扇形S2的圆心角为240度,
则它的弧长= =2πR2,R2=
=2πR2,R2= ,
,
由勾股定理得,h2= r;
r;
设扇形S1做成圆锥的底面半径为R1,
由题意知,扇形S1的圆心角为120度,
则它的弧长= =2πR1,R1=
=2πR1,R1=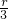 ,
,
由勾股定理得,h1= r,
r,
∴h1>h2,
故选A.
点评:本题利用了勾股定理,弧长公式,圆的周长公式求解.
分析:利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径和母线长的关系,进而利用勾股定理可求得各个圆锥的高,比较即可.
解答:设扇形S2做成圆锥的底面半径为R2,
由题意知,扇形S2的圆心角为240度,
则它的弧长=
 =2πR2,R2=
=2πR2,R2= ,
,由勾股定理得,h2=
 r;
r;设扇形S1做成圆锥的底面半径为R1,
由题意知,扇形S1的圆心角为120度,
则它的弧长=
 =2πR1,R1=
=2πR1,R1=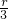 ,
,由勾股定理得,h1=
 r,
r,∴h1>h2,
故选A.
点评:本题利用了勾股定理,弧长公式,圆的周长公式求解.

练习册系列答案
相关题目
 如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为
如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为 只有一个实数解,则k的值是
只有一个实数解,则k的值是 如图,将一长方形从一顶点到不相邻的另一顶点,任意画线得A、B两图形,下列说法正确的是
如图,将一长方形从一顶点到不相邻的另一顶点,任意画线得A、B两图形,下列说法正确的是 ㎡
㎡ ㎡
㎡ ㎡
㎡ ㎡
㎡ 如图,反比例函数
如图,反比例函数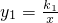 和一次函数y2=k2x+b的图象在第一象限内交于点A,且点A 横坐标为2,若0<y2<y1,则x的取值范围是
和一次函数y2=k2x+b的图象在第一象限内交于点A,且点A 横坐标为2,若0<y2<y1,则x的取值范围是 |,
|, ,π,
,π, ,
, ,
,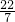 中无理数有几个
中无理数有几个


