题目内容
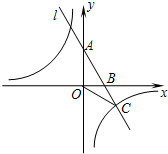 如图,过点B(2,0)的直线l:
如图,过点B(2,0)的直线l: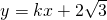 交y轴于点A,与反比例函数y=
交y轴于点A,与反比例函数y= 的图象交于点C(3,n).
的图象交于点C(3,n).
(1)求反比例函数的解析式;
(2)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′.当OC′⊥AB时,求点C运动的路径长.
解:(1)∵点B(2,0)在直线l: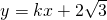 上,
上,
∴2k+2 =0,
=0,
∴k=- ,
,
直线l的解析式为:y=- x+2
x+2 ,
,
∵点C(3,n)在直线y=- x+2
x+2 上,
上,
∴- ×3+2
×3+2 =n,
=n,
n=- ,
,
∴C点坐标是(3,- ),
),
∵C(3,- )在反比例函数y=
)在反比例函数y= 的图象上,
的图象上,
∴m=-3 ,
,
∴反比例函数的解析式是:y=-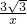 ;
;
(2)过C点作CE⊥x轴于E,如图,
∵C点坐标是(3,- ),
),
∴OC=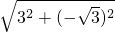 =2
=2 ,
,
∵点A是直线y=- x+2
x+2 与y轴交点,
与y轴交点,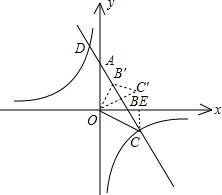
∴AO=2 ,
,
∵AO=CO,
∴∠ACO=∠OAC,
又∵OB=2,
∴AB= =4,
=4,
∴∠OAB=30°,
∴∠ACO=30°,
∵OC′⊥AB,
∴∠C′OC=60°,
点C的运动路径的长度=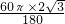 =
=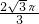 .
.
分析:(1)利用待定系数法把B(2,0)代入直线l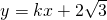 的解析式可以算出k的值,继而得到直线l的解析式,再把C点坐标代入直线l的解析式可以算出C点坐标,再把C点坐标代入反比例函数y=
的解析式可以算出k的值,继而得到直线l的解析式,再把C点坐标代入直线l的解析式可以算出C点坐标,再把C点坐标代入反比例函数y= 即可得到反比例函数的解析式;
即可得到反比例函数的解析式;
(2)首先根据题意画出图形,证明AO=CO,根据等边对等角可得∠ACO=∠OAC,再利用勾股定理计算出AB的长,继而得到∠OAC的度数,也就是得到了∠ACO的度数,再由条件OC′⊥AB计算出∠C′OC的度数,再根据弧长公式计算出点C运动的路径长.
点评:此题主要考查了利用待定系数法求一次函数、反比例函数关系式,以及旋转和弧长公式,关键是掌握凡是图象经过的点都能满足解析式,求出∠C′OC的度数是解决第二问的关键.
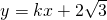 上,
上,∴2k+2
 =0,
=0,∴k=-
 ,
,直线l的解析式为:y=-
 x+2
x+2 ,
,∵点C(3,n)在直线y=-
 x+2
x+2 上,
上,∴-
 ×3+2
×3+2 =n,
=n,n=-
 ,
,∴C点坐标是(3,-
 ),
),∵C(3,-
 )在反比例函数y=
)在反比例函数y= 的图象上,
的图象上,∴m=-3
 ,
,∴反比例函数的解析式是:y=-
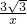 ;
;(2)过C点作CE⊥x轴于E,如图,
∵C点坐标是(3,-
 ),
),∴OC=
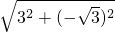 =2
=2 ,
,∵点A是直线y=-
 x+2
x+2 与y轴交点,
与y轴交点,
∴AO=2
 ,
,∵AO=CO,
∴∠ACO=∠OAC,
又∵OB=2,
∴AB=
 =4,
=4,∴∠OAB=30°,
∴∠ACO=30°,
∵OC′⊥AB,
∴∠C′OC=60°,
点C的运动路径的长度=
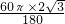 =
=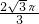 .
.分析:(1)利用待定系数法把B(2,0)代入直线l
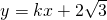 的解析式可以算出k的值,继而得到直线l的解析式,再把C点坐标代入直线l的解析式可以算出C点坐标,再把C点坐标代入反比例函数y=
的解析式可以算出k的值,继而得到直线l的解析式,再把C点坐标代入直线l的解析式可以算出C点坐标,再把C点坐标代入反比例函数y= 即可得到反比例函数的解析式;
即可得到反比例函数的解析式;(2)首先根据题意画出图形,证明AO=CO,根据等边对等角可得∠ACO=∠OAC,再利用勾股定理计算出AB的长,继而得到∠OAC的度数,也就是得到了∠ACO的度数,再由条件OC′⊥AB计算出∠C′OC的度数,再根据弧长公式计算出点C运动的路径长.
点评:此题主要考查了利用待定系数法求一次函数、反比例函数关系式,以及旋转和弧长公式,关键是掌握凡是图象经过的点都能满足解析式,求出∠C′OC的度数是解决第二问的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,过点O、A(1,0)、B(0,
如图,过点O、A(1,0)、B(0,| 3 |
| A、60° |
| B、60°或120° |
| C、30° |
| D、30°或150° |
 8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
 如图,过点P(2,
如图,过点P(2, 如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例
如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例