题目内容
【题目】(操作)BD是矩形ABCD的对角线,![]() ,
,![]() ,将
,将![]() 绕着点B顺时针旋转
绕着点B顺时针旋转![]() (
(![]() )得到
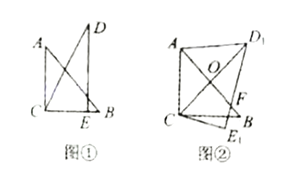
)得到![]() ,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则
,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则![]() ________.
________.
(探究)当点E落在线段DF上时,CD与BE交于点C.其它条件不变,如图②.
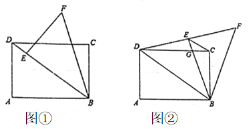
(1)求证:![]() ;
;
(2)CG的长为________.
【答案】【操作】1;【探究】(1)见解析;(2)CG的长为![]() .
.
【解析】
[操作]由勾股定理求出BD,由旋转的性质得到![]() ,即可求出ED;
,即可求出ED;
[探究](1)由旋转的性质得对应边相等,对应角相等,然后利用斜边直角边判定![]() ;
;
(2)由平行线得到内错角![]() ,再由(1)的全等可得
,再由(1)的全等可得![]() ,从而得到
,从而得到![]() ,所以
,所以![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中,由勾股定理建立方程求解即可.
中,由勾股定理建立方程求解即可.
[操作] 解:∵四边形ABCD是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由旋转的性质得:![]() ,
,
∴![]() ;
;
故答案为:1;
[探究](1)证明:由旋转的性质得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
∴![]() ;
;
(2)解:∵四边形ABCD是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由(1)得:![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
解得:![]() ,即
,即![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目