题目内容
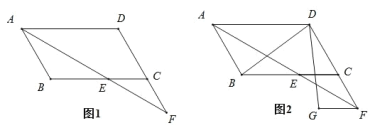
【题目】把一副三角板如图①放置，其中
，斜边
，把三角板
绕点
顺时针旋转
，得到
，如图②，这时
与
相交于点
，与
相交于点
.
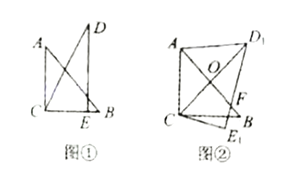
（1）求
的度数；
（2）求线段
的长；
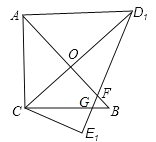
（3）若把绕着点顺时针再旋转
，得
.这时点
在的内部、外部，还是边上？请说明理由，
【答案】（1）
；（2）
；（3）
在
的内部
【解析】
（1）设D1E1与BC交于点G，先求出∠CGE1，再根据对顶角相等求出∠FGB，即可求解．
（2）先证明OA=OC，∠AOC=90°，在Rt△AOD中，利用勾股定理求解．
（3）设直线CB交D2E2于点M，求出CM与BC的长度，再比较即可判断．
（1）设
与
交于点
，
在
中，
又
；
（2）由旋转知
，
，
又∵
，
，
∴由勾股定理可得：
；
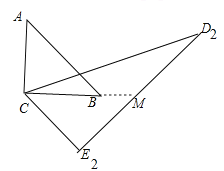
（3）设直线
交
于点
，
，
，
又∵
，
∴点在的内部.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
