Question

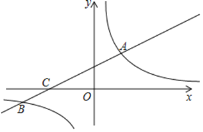
【题目】如图，在平面直角坐标系中，直线与双曲线相交于点，，与轴交于点．

（1）求直线的解析式；

（2）若点在轴上，且，求点的坐标．

Answer 1

【答案】（1）y＝x+2；（2）点P的坐标为（﹣6，0）或（﹣2，0）．

【解析】

（1）求直线的解析式，就是求其中k,b的值，待定系数法即可，但需要找到两个点，发现A,B两个点在直线上，只需要知道A,B两点的坐标即可，因为A,B同时在双曲线上，代入双曲线方程即可求出A,B的坐标，进而可求出直线的解析式；

（2）因为P点在轴上，可以把P的坐标设为，利用两个三角形面积之间的关系，找到关于的方程即可求出x的值.

解：（1）∵点A（m，3），B（﹣6，n）在双曲线y＝上，

∴m＝2，n＝﹣1，

∴A（2，3），B（﹣6，﹣1）．

将（2，3），B（﹣6，﹣1）代入y＝kx+b，

得

解得．

∴直线的解析式为y＝x+2．

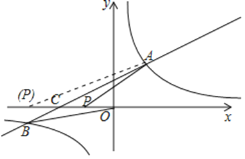
（2）当y＝x+2＝0时，x＝﹣4，

∴点C（﹣4，0）．

设点P的坐标为（x，0），

∵S△ACP＝S△BOC，A（2，3），B（﹣6，﹣1），

∴×3×|x﹣（﹣4）|＝××|0﹣（﹣4）|×|﹣1|，即|x+4|＝2，

解得：x1＝﹣6，x2＝﹣2．

∴点P的坐标为（﹣6，0）或（﹣2，0）．