题目内容
18. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上的一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是1.
如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上的一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是1.
分析 根据圆周角定理得到∠D=90°,根据勾股定理求出BD、证明△ADE∽△BCE,得到BE=5AE,根据勾股定理计算即可.
解答 解:在等腰Rt△ABC中,BC=4,
∴AB是⊙O的直径,AB=4$\sqrt{2}$,
∴∠D=90°,
∵AD=$\frac{4}{5}$,AB=4$\sqrt{2}$,
∴BD=$\frac{28}{5}$,
∵∠D=∠C,∠DAC=∠CBE,
∴△ADE∽△BCE,
∴$\frac{AE}{BE}$=$\frac{AD}{BC}$=$\frac{1}{5}$,即BE=5AE,
在Rt△BCE中,CE2+BC2=BE2,即(4-AE)2+42=(5AE)2,
解得,AE=1,
故答案为:1.
点评 本题考查的是三角形的外接圆与外心、相似三角形的判定和性质,掌握圆周角定理、相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
9.小颖的妈妈在某玩具厂工作,厂里规定每个工人每周要生产某种玩具140个,平均每天生产20个,但由于种种原因,实际每天生产量与计划量相比有出入.下表是小颖妈妈某周的生产情况(超产记为正、减产记为负):
根据记录的数据求:
(1)小颖妈妈星期三生产玩具多少个?
(2)本周实际生产玩具多少个?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
(1)小颖妈妈星期三生产玩具多少个?
(2)本周实际生产玩具多少个?
3. 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,点P第1次碰到矩形的边时,点P的坐标是(3,0),则当点P第2016次碰到矩形的边时,点P的坐标是( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,点P第1次碰到矩形的边时,点P的坐标是(3,0),则当点P第2016次碰到矩形的边时,点P的坐标是( )
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,点P第1次碰到矩形的边时,点P的坐标是(3,0),则当点P第2016次碰到矩形的边时,点P的坐标是( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,点P第1次碰到矩形的边时,点P的坐标是(3,0),则当点P第2016次碰到矩形的边时,点P的坐标是( )| A. | (1,4) | B. | (0,3) | C. | (5,0) | D. | (8,3) |
8.只用下列多边形,不能进行平面镶嵌的是( )
| A. | 三角形 | B. | 四边形 | C. | 正六边形 | D. | 正八边形 |
 [问题提出]
[问题提出]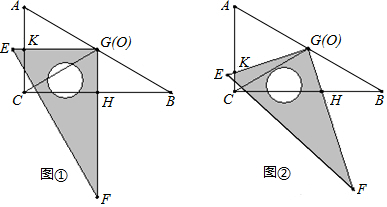
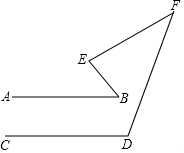 已知,如图,∠E=80°,且$\sqrt{∠B-n-20°}$+(∠D-80°-n)2+|∠F-40°|=0.(n为常数,且0°<n<100°).
已知,如图,∠E=80°,且$\sqrt{∠B-n-20°}$+(∠D-80°-n)2+|∠F-40°|=0.(n为常数,且0°<n<100°).