题目内容
 16、根据图形填空:
16、根据图形填空:(1)∠AOC=∠AOB+∠
BOC
;(2)∠COD=∠AOD-∠
AOC
;(3)∠BOC=∠
BOD
-∠COD;(4)∠AOB+∠COD=∠
AOD
-∠BOC
.分析:(1)本题需先结合图象,再根据角的特点及概念分别得出答案.
(2)本题需先结合图形,再有图形得出角的组成即可求出答案.
(3)本题需先结合图形看看∠BOC有那几个角组成,再进行相减即可求出答案.
(4)本题需先结合图形看出∠AOB+∠COD是那个角,再根据角的特点即可求出答案.
(2)本题需先结合图形,再有图形得出角的组成即可求出答案.
(3)本题需先结合图形看看∠BOC有那几个角组成,再进行相减即可求出答案.
(4)本题需先结合图形看出∠AOB+∠COD是那个角,再根据角的特点即可求出答案.
解答:解:(1)有图形可知
∵∠AOC=∠AOB+∠BOC,
故答案为:∠BOC;
(2)∵∠COD=∠AOD-∠AOC,
故答案为:∠AOC;
(3)∵∠BOC=∠BOD-∠COD,
故答案为:∠BOD;
(4)∵∠AOB+∠COD=∠AOD-∠BOC,
故答案为:∠AOD、∠BOC.
∵∠AOC=∠AOB+∠BOC,
故答案为:∠BOC;
(2)∵∠COD=∠AOD-∠AOC,
故答案为:∠AOC;
(3)∵∠BOC=∠BOD-∠COD,
故答案为:∠BOD;
(4)∵∠AOB+∠COD=∠AOD-∠BOC,
故答案为:∠AOD、∠BOC.
点评:本题主要考查了角的计算,在解题时要结合图形和角的组成是本题的关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
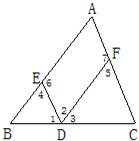 15、如图,根据图形填空
15、如图,根据图形填空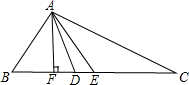 如图,根据图形填空:
如图,根据图形填空: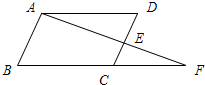 24、如图,根据图形填空:
24、如图,根据图形填空: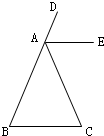 24、根据图形填空:
24、根据图形填空: