题目内容
 24、根据图形填空:
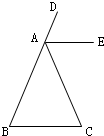
24、根据图形填空:已知:AD是线段BA的延长线,AE平分∠DAC,AE∥BC,那么∠B与∠C相等吗?
解:∵AE平分∠DAC (
已知
)∴∠DAE=∠CAE (
角平分线的性质
)∵AE∥BC (
已知
)∴∠DAE=∠B (
两直线平行,同位角相等
)∠CAE=∠C (
两直线平行,内错角相等
)∴∠B=∠C (
等量代换
)分析:根据已知条件,利用角平分线的性质可得∠DAE=∠CAE,再利用平行线的性质和等量代换求证结论.
解答:解:∵已知中已注明,AE平分∠DAC,
∴利用角平分线的性质可得∠DAE=∠CAE,
再根据已知条件AE∥BC,
利用两直线平行,同位角相,等两直线平行,同位角相等,
和等量代换即可证明∠B=∠C.
故答案为:已知;角平分线的性质;已知;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.
∴利用角平分线的性质可得∠DAE=∠CAE,
再根据已知条件AE∥BC,
利用两直线平行,同位角相,等两直线平行,同位角相等,
和等量代换即可证明∠B=∠C.
故答案为:已知;角平分线的性质;已知;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.
点评:此题主要考查学生对平行线性质的理解与掌握,难度不大,属于基础题,要求学生应熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
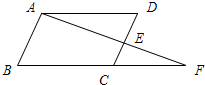 24、如图,根据图形填空:
24、如图,根据图形填空: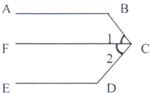 29、如图,根据图形填空:
29、如图,根据图形填空: 根据图形填空:
根据图形填空: