Question

【题目】如图，△ABC中，∠ACB＝90°，AC＝8，BC＝6，分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，连接EF、ND，则图中阴影部分的面积之和等于_____．

Answer 1

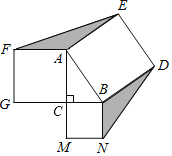
【答案】48

【解析】

如图将△FAE绕点A顺时针旋转90°得到△KAB．首先证明S△ABK＝S△ABC＝S△AFE，同理可证S△BDN＝S△ABC，推出S△AEF+S△BDN＝2S△ABC，由此即可解决问题．

如图将△FAE绕点A顺时针旋转90°得到△KAB．

∵∠FAC＝∠EAB＝90°，

∴∠FAE+∠CAB＝180°，

∵∠FAE＝∠KAB，

∴∠KAB+∠CAB＝180°，

∴C、A、K共线，

∵AF＝AK＝AC，

∴S△ABK＝S△ABC＝S△AFE，

同理可证S△BDN＝S△ABC，

∴S△AEF+S△BDN＝2S△ABC＝2××6×8＝48，

故答案为：48．