��Ŀ����
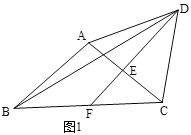
����Ŀ������ABC�У�AB=AC������ABC���ⲿ���ȱ���������ACD��EΪAC���е㣬����DE���ӳ���BC�ڵ�F������BD��
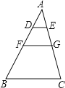
��1����ͼ1������BAC=100�������ABD�Ķ���Ϊ_____����BDF�Ķ���Ϊ______��
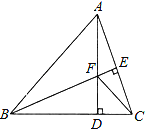
��2����ͼ2����ACB��ƽ���߽�AB�ڵ�M����EF�ڵ�N������BN����BN=DN����ACB=![]() ��
��
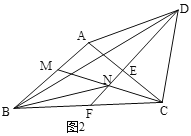
(I)��![]() ��ʾ��BAD��
��ʾ��BAD��
(II)����֤����ABN=30����
��ֱ��д��![]() �Ķ����Լ���BMN����״��
�Ķ����Լ���BMN����״��
���𰸡�(1)10����20������2������![]() ��(II)��֤������������
��(II)��֤������������![]() =40������BMN���������Σ�
=40������BMN����������
��������
��1���ɵȱ������ε����ʿɵ�AD=AC����CAD=60�������õ��������ɵ�AD=AB�����ݵ��������ε����ʼ��������ABD�Ķ������ɵ��������������ߺ�һ�������ʿɵá�ADE=30���������������BDF�Ķ�����
��2�������ݵ��������ε����ʿ���![]() ��ʾ����BAC���ɡ�CAD=60�����ɱ�ʾ����BAD��
��ʾ����BAC���ɡ�CAD=60�����ɱ�ʾ����BAD��
������ͼ������AN���ɽ�ƽ���ߵĶ���ɵá�CAN=![]()
![]() �����ݵ��������������ߺ�һ�������ʿɵ�DN��AC�Ĵ�ֱƽ���ߣ��ɵ�AN=CN����CAN=��CAN�����������DAN=
�����ݵ��������������ߺ�һ�������ʿɵ�DN��AC�Ĵ�ֱƽ���ߣ��ɵ�AN=CN����CAN=��CAN�����������DAN=![]()
![]() +60�����ɣ���֪��BAD=240��-2
+60�����ɣ���֪��BAD=240��-2![]() ���ɡ�ABN�ա�AND�ɵá�BAN=��DAN���ɵá�BAN=120��+
���ɡ�ABN�ա�AND�ɵá�BAN=��DAN���ɵá�BAN=120��+![]() ���з��̼������
���з��̼������![]() ��ֵ������������ʿ������ANM�Ķ����������������ڽǺͿ������AMN�Ķ���������������ʿ������MNB�Ķ������ɵá�BMN=��ABN����֤����BMN�ǵ��������Σ�
��ֵ������������ʿ������ANM�Ķ����������������ڽǺͿ������AMN�Ķ���������������ʿ������MNB�Ķ������ɵá�BMN=��ABN����֤����BMN�ǵ��������Σ�
��1���ߡ�ACD�ǵȱ������Σ�
��AD=AC=CD����CAD=��ADC=60����
��AB=AC��
��AD=AB��
�ߡ�BAC=100����
���BAD=��BAC+��CAD=160����
���ABD=��ADB=![]() ��180��-��BAD��=10����
��180��-��BAD��=10����
�ߵ�EΪAC�е㣬
�� ��ADE=��CDE=30����
���BDF=��ADE-��ADB=20����
�ʴ�Ϊ��10����20��
��2������AB=AC����ACB=![]() ��
��
���ABC=��ACB=![]() ��
��
��![]() ��
��
�ߡ�ACDΪ�ȱ������Σ�
���CAD=60����
���BAD=��BAC+��CAD=240��+![]() ��
��
(II)����ͼ������![]() ��
��
�ߡ�ACDΪ�ȱ������Σ�
��![]() ��
��
�ڡ�ABN�͡�AND�У� ��
��
���ABN�ա�AND��
���ABN=��ADN��
�ߵ�E![]() ���е㣬
���е㣬
��DF��AC��EDƽ�֡�ADC��
���ADE=30����
���ABN=��ADE=30����

�ڡ�CMƽ�֡�ACB����ACB=![]() ��
��
���CAM=��BCM=![]()
![]() ��
��
�ߵ�E��AC���е㣬��ACD�ǵȱ������Σ�
��DN��AC�Ĵ�ֱƽ���ߣ�
��AN=CN��
���CAN=��ACM=![]()
![]() ��
��
���DAN=��CAD+��CAN=60��+![]()
![]() ��
��
�ߡ�ABN�ա�AND��
���BAN=��DAN=60��+![]()
![]() ��
��
���BAN=2��BAN=120��+![]() ��
��
�ɣ��ã���BAD=240��-2![]() ��
��
��120��+![]() =240��-2
=240��-2![]() ��
��
��ã�![]() =40����
=40����
���BAN=60��+![]()
![]() =80������ANM=��NAC+��NCA=
=80������ANM=��NAC+��NCA=![]() =40����
=40����
���AMC=180��-��BAN-��ANM=60����
�ߡ�ABN=30����
���MNB=��AMC-��ABN=30����
���ABN=��MNB��
��MB=MN��
��![]() �ǵ��������Σ�
�ǵ��������Σ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�