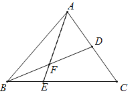
题目内容
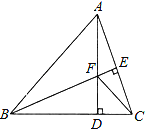
【题目】如图,在![]() 中,
中,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 交于点
交于点![]() ,
,![]() .若
.若![]() 的面积为18,给出下列命题:①
的面积为18,给出下列命题:①![]() 的面积为16;②
的面积为16;②![]() 的面积和四边形
的面积和四边形![]() 的面积相等;③点
的面积相等;③点![]() 是
是![]() 的中点;④四边形
的中点;④四边形![]() 的面积为
的面积为![]() ;其中,正确的结论有_____________.
;其中,正确的结论有_____________.
【答案】③④
【解析】
①根据等高的三角形面积比等于底边比即可求解;②先分别得出△ABE的面积与△BCD的面积的关系,然后进一步求解即可;③过点D作DG∥BC,通过三角形中位线性质以及全等三角形的判定和性质进一步求解即可;④根据题意将该四边形面积计算出来即可.据此选出正确的选项从而得出答案.
① ∵![]() ,
,
∴EB=![]() BC,
BC,
∴![]() 的面积=
的面积=![]() ,
,
故①错误;
② ∵![]() ,点D为AC的中点,
,点D为AC的中点,
∴△ABE的面积≠△BCD的面积,
∴![]() 的面积和四边形
的面积和四边形![]() 的面积不相等,
的面积不相等,
故②错误;
③ 如图,过点D作DG∥BC,
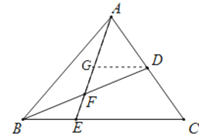
∵D是AC中点,DG∥BC,
∴DG=![]() ,
,
∵![]() ,
,
∴DG=EB,
∵DG∥BC,
∴∠DGF=∠BEF,∠GDF=∠EBF,
在△DGF与△BEF中,
∵∠DGF=∠BEF,DG=EB,∠GDF=∠EBF,
∴△DGF≌△BEF(ASA),
∴DF=BF,
∴点![]() 是
是![]() 的中点,
的中点,
故③正确;
④ 四边形![]() 的面积=
的面积=![]() ,
,
故④正确;
综上所述,正确的结论有:③④,
故答案为:③④.

练习册系列答案
相关题目