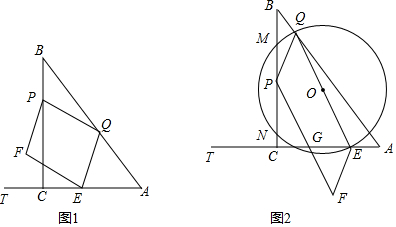��Ŀ����
9��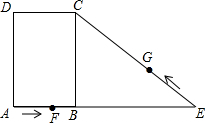 �ھ���ABCD�У�AB=4cm��AD=6cm���ӳ�AB��E��ʹBE=2AB������CE������F��A������2cm/s���ٶ���AE�������E�˶�������G��E���������3cm/s���ٶ���E��C��D�������D�˶�����������ͬʱ������������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ���趯���˶���ʱ��Ϊt�룮
�ھ���ABCD�У�AB=4cm��AD=6cm���ӳ�AB��E��ʹBE=2AB������CE������F��A������2cm/s���ٶ���AE�������E�˶�������G��E���������3cm/s���ٶ���E��C��D�������D�˶�����������ͬʱ������������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ���趯���˶���ʱ��Ϊt�룮��1����tΪ��ֵʱ��FC��EG����ƽ�֣�
��2������FG����t��$\frac{10}{3}$ʱ���Ƿ����ʱ��tʹ��EFG���EBC���ƣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��3�����EFG�����Ϊy�����y��t�ĺ�����ϵʽ����tΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
���� ��1�����жϳ��ı���CEFG��ƽ���ı��Σ����öԱ���Ƚ���������⼴�ɵó����ۣ�
��2����������������������εĶ�Ӧ�߳ɱ�������������⼴�ɣ�
��3���ֵ�G��CE��CD�ϣ��������ε�������ɣ�
��� �⣺��1����ͼ1��
��AB=4����BE=2AB=8��
��Rt��BCE�У����ݹ��ɶ����ã�CE=10��
���˶�֪��CG=3t-10��EF=AB+BE-2t=12-2t��
��FC��EG����ƽ�֣�
���G����CD���ϣ�
���ı���CEFG��ƽ���ı��Σ�
��CG=EF��
��3t-10=12-2t��
��t=$\frac{22}{5}$��
��2���ߵ�t��$\frac{10}{3}$ʱ����G��CE�ϣ�
�ߡ�EFG���EBC���ƣ�
����EFG�ס�EBCʱ�� ��$\frac{EF}{BE}=\frac{EG}{EC}$��
��$\frac{EF}{BE}=\frac{EG}{EC}$��
��$\frac{12-2t}{8}=\frac{3t}{10}$��
��t=$\frac{30}{11}$��
����EGF�ס�EBCʱ��
��$\frac{EG}{BE}=\frac{EF}{EC}$��
��$\frac{3t}{8}=\frac{12-2t}{10}$��
��t=$\frac{48}{23}$��
��3������G��CE��ʱ������0��t��$\frac{10}{3}$����ͼ3��
����G��GM��BE��
��GM��BC��
���EMG�ס�EBC��
��$\frac{GM}{BC}=\frac{EG}{EC}$��
��$\frac{GM}{6}=\frac{3t}{10}$��
��GM=$\frac{9}{5}$t��
��y=S��EFG=$\frac{1}{2}$EF•GM=$\frac{1}{2}$����12-2t����$\frac{9}{5}$t=-$\frac{9}{5}$t2+$\frac{54}{5}$t=-$\frac{9}{5}$��t-3��2+$\frac{81}{5}$��
��t=3ʱ��y���=$\frac{81}{5}$��
����G��CD��ʱ������$\frac{10}{3}$��t��$\frac{14}{3}$��
y=S��EFG=$\frac{1}{2}$EF��BC=$\frac{1}{2}$��12-2t����6=-6t+36��
����t=3ʱ��y���=$\frac{81}{5}$��
���� ���������������ε��ۺ��⣬��Ҫ���������������ε����ʺ��ж���ƽ���ı��ε��ж������ʣ������ε������ʽ���÷��̵�˼���ǽⱾ��Ĺؼ���ע��������۵�˼���Ӧ�ã�

| A�� | a2+a3=a5 | B�� | a3-a2=a | C�� | a2•a3=a6 | D�� | a3��a2=a |
| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 2 |
| A�� | 2 | B�� | -2 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
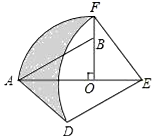 ��ͼ����Rt��AOB�У���AOB=90�㣬OA=2��OB=1����Rt��AOB�Ƶ�O˳ʱ����ת90����Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90�����߶�ED���ֱ���O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ��������ǣ�������
��ͼ����Rt��AOB�У���AOB=90�㣬OA=2��OB=1����Rt��AOB�Ƶ�O˳ʱ����ת90����Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90�����߶�ED���ֱ���O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ��������ǣ�������| A�� | �� | B�� | ��+5 | C�� | $\frac{14-��}{4}$ | D�� | $\frac{10-��}{4}$ |
 ��ͼ����֪AB�ǡ�O��ֱ������CAB=50�㣬���D�Ķ���Ϊ��������
��ͼ����֪AB�ǡ�O��ֱ������CAB=50�㣬���D�Ķ���Ϊ��������| A�� | 20�� | B�� | 40�� | C�� | 50�� | D�� | 70�� |
| A�� | 2.11��104 | B�� | 2.12��104 | C�� | 0.212��105 | D�� | 0.21��105 |