题目内容
14.已知:如图1所示,在菱形ABCD中,以AB为直径的⊙O交AC于点E,EF⊥BC于点F.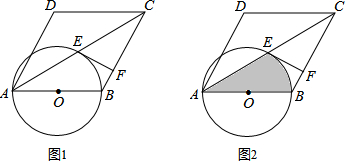
(1)求证:EF是⊙O的切线;
(2)若菱形的边长为4,∠ABC=120°,求出AC的值;
(3)在第(2)问的条件下,求图2中阴影部分的面积.
分析 (1)连接OE,先证明OE∥BC,再由EF⊥BC,得出EF⊥OE,即可证出EF是⊙O的切线;
(2)连接BE,先由菱形的性质得出BE⊥AC,∠BCA=∠BAC=30°,再根据三角函数求出AE,即可得出AC;
(3)作EG⊥AB于G,先求出EG,阴影部分的面积=△AOE的面积+扇形OBE的面积.
解答 (1)证明:连接OE,如图1所示: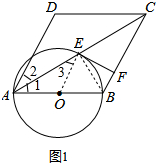 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC,∠1=∠2,
∵OA=OE,
∴∠1=∠3,
∴OE∥BC,
∵EF⊥BC,
∴EF⊥OE,
∴EF是⊙O的切线;
(2)解:连接BE、OE,如图1所示: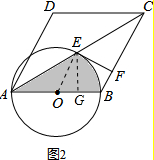 则∠ABE=90°,
则∠ABE=90°,
∵AB=BC=4,∠ABC=120°,
∴BE⊥AC,∠BCA=∠BAC=30°,
∴AE=AB•cos∠BAC=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴AC=2AE=4$\sqrt{3}$;
(3)解:作EG⊥AB于G,如图2所示:
则EG=$\frac{1}{2}$AE=$\sqrt{3}$,
∵OA=$\frac{1}{2}$AB=2,
∴阴影部分的面积=△AOE的面积+扇形OBE的面积=$\frac{1}{2}$×2×$\sqrt{3}$+$\frac{60π×{2}^{2}}{360}$=$\sqrt{3}$+$\frac{2π}{3}$.
点评 本题考查了切线的判定、菱形的性质、锐角三角函数、圆周角定理以及扇形面积的计算方法;熟练掌握切线的判定和菱形的性质,并能进行有关运算是解决问题的关键.

练习册系列答案
相关题目
9.若把分式$\frac{a-2b}{abc}$中的a,b,c都扩大到原来的2倍,则分式的值( )
| A. | 不变 | B. | 扩大到原来的2倍 | C. | 缩小到原来的$\frac{1}{4}$ | D. | 缩小到原来的$\frac{1}{9}$ |
6.$\sqrt{4}$的算术平方根是( )
| A. | 4 | B. | 2 | C. | $\sqrt{2}$ | D. | ±2 |
3.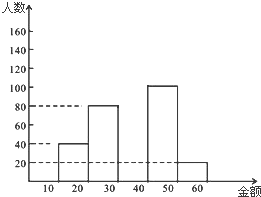 四川雅安地震发生后,某校开展了为灾区捐款的活动.小明把本年级同学的捐款情况统计并制成图表,如图:
四川雅安地震发生后,某校开展了为灾区捐款的活动.小明把本年级同学的捐款情况统计并制成图表,如图:
请根据图表提供的信息解答下列问题:
(1)表中m和n所表示的数分别是多少?M=160,n0.25.
(2)补全频数分布直方图;
(3)该校共有学生3000人,试估计全校为灾区捐款40元以上(包含40元)的学生人数.
 四川雅安地震发生后,某校开展了为灾区捐款的活动.小明把本年级同学的捐款情况统计并制成图表,如图:
四川雅安地震发生后,某校开展了为灾区捐款的活动.小明把本年级同学的捐款情况统计并制成图表,如图:| 金额(元) | 人数 | 频率 |
| 10≤x<20 | 40 | 0.1 |
| 20≤x<30 | 80 | 0.2 |
| 30≤x<40 | m | 0.4 |
| 40≤x<50 | 100 | n |
| 50≤x<60 | 20 | 0.05 |
(1)表中m和n所表示的数分别是多少?M=160,n0.25.
(2)补全频数分布直方图;
(3)该校共有学生3000人,试估计全校为灾区捐款40元以上(包含40元)的学生人数.
 如图,Rt△ABC在直角坐标系中,AB与y轴交于点F,直线AB的解析式为y=$\frac{1}{2}$x+1,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与BC边交于点D(4,1),与AB边交于点E(2,n),点P是射线FD上一点,△FEP与△AEO相似,则点P的坐标为(1,1)或(5,1).
如图,Rt△ABC在直角坐标系中,AB与y轴交于点F,直线AB的解析式为y=$\frac{1}{2}$x+1,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与BC边交于点D(4,1),与AB边交于点E(2,n),点P是射线FD上一点,△FEP与△AEO相似,则点P的坐标为(1,1)或(5,1).