题目内容
14.关于x,y的方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$,当a满足什么条件时,x+y>0?分析 首先应用加减法,求出关于x,y的方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$的解,然后把求出的x、y的值代入x+y>0,再根据一元一次不等式的求解方法,求出a满足什么条件即可.
解答 解:∵$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=2a+1}\\{y=a-2}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=2a+1}\\{y=a-2}\end{array}\right.$代入x+y>0,可得
(2a+1)+(a-2)>0,
∴3a-1>0,
解得a>$\frac{1}{3}$,
即a$>\frac{1}{3}$时,x+y>0.
点评 (1)此题主要考查了二元一次方程组的求法,要掌握两种常用的方法:加减法和代入法.
(2)此题还考查了一元一次不等式的求解,解答此题的关键是要明确其基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.

练习册系列答案
相关题目
8. 如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
 如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 140° |
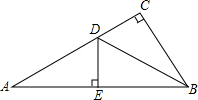 如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,如果∠A=30°,DE=4cm,求∠DBC的度数和CD的长.
如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,如果∠A=30°,DE=4cm,求∠DBC的度数和CD的长.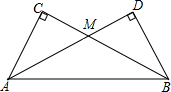 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?