题目内容
7. 如图:已知P是半径为5cm的⊙O内一点.解答下列问题:
如图:已知P是半径为5cm的⊙O内一点.解答下列问题:(1)用尺规作图找出圆心O的位置.要求:保留所有的作图痕迹,不写作法.
(2)用三角板分别画出过点P的最长弦AB和最短弦CD.
(3)已知OP=3cm,过点P的弦中,长度为整数的弦共有4条.
分析 (1)利用过不在同一直线上的三点可以确定一个圆,进而求出即可;
(2)利用最长弦AB即为直径和最短弦CD,即为与AB垂直的弦,进而得出答案;
(3)求出CD的长,进而得出长度为整数的弦,注意长度为9cm,的有两条.
解答  解:(1)如图所示:点O即为所求;
解:(1)如图所示:点O即为所求;
(2)如图所示:AB,CD即为所求;
(3)如图:连接DO,
∵OP=3cm,DO=5cm,
∴在Rt△OPD中,DP=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm),
∴CD=8cm,
∴过点P的弦中,长度为整数的弦共有:4条.
故答案为:4.
点评 此题主要考查了复杂作图以及勾股定理和垂径定理,注意长度为整数的弦不要漏解.

练习册系列答案
相关题目
2.方程(x-1)(x+2)=2(x+2)的根是( )
| A. | 1,-2 | B. | 3,-2 | C. | 0,-2 | D. | 1,2 |
 如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )
如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )
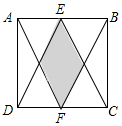 如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积是$\frac{1}{4}$.
如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积是$\frac{1}{4}$.