Question

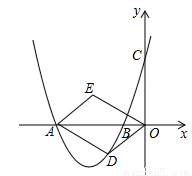
如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋3与x轴交于点A（－4，0），B（－1，0）两点．

（1）求抛物线的解析式；

（2）在第三象限的抛物线上有一动点D．如图，若四边形ODAE是以OA为对角线的平行四边形，当平行四边形ODAE的面积为6时，请判断平行四边形ODAE是否为菱形？说明理由．

Answer 1

（1）y=x2+x+3．；（2）当点D为（-2，-）时，DH垂直平分OA，平行四边形ODAE为菱形；当点D为（-3，-）时，OD≠AD，平行四边形ODAE不为菱形．

【解析】

试题分析：（1）利用待定系数法求出抛物线的解析式；

（2）本问需结合菱形、平行四边形的性质来进行分析．如图，作辅助线，求出点D的坐标，进而判断平行四边形ODAE是否为菱形.

试题解析：（1）把点A（-4，0）、B（-1，0）代入解析式y=ax2+bx+3，

得

，

解得，

∴抛物线的解析式为：y=x2+x+3．

（2）如图，过点D作DH⊥x轴于点H．

∵S?ODAE=6，OA=4，

∴S△AOD=OA•DH=3，

∴DH=．

因为D在第三象限，所以D的纵坐标为负，且D在抛物线上，

∴x2+x+3=-，

解得：x1=-2，x2=-3．

∴点D坐标为（-2，-）或（-3，-）．

当点D为（-2，-）时，DH垂直平分OA，平行四边形ODAE为菱形；

当点D为（-3，-）时，OD≠AD，平行四边形ODAE不为菱形．

考点：二次函数综合题．