题目内容
已知:在等腰梯形ABCD中,DC∥AB,AD=BC=10,DC=13 ,tanA=
,tanA=| 3 | 4 |
(1)求AB的长;
(2)设点E是线段AB上的点,当BE等于多少时,△AED与△BCE相似?
分析:(1)作辅助线DF⊥AB,CH⊥AB垂足分别为F、G,利用三角函数以及勾股定理求出DF,AF,AB的值.
(2)证明△ADE∽△BCE(
=
得出BE=
AB),再证明△ADE∽△BEC得出BE(AB-BE)=AD•BC,求出BE.
(2)证明△ADE∽△BCE(
| AD |
| BC |
| AE |
| BE |
| 1 |
| 2 |
解答: 解:(1)作DF⊥AB,CH⊥AB垂足分别为F、G.
解:(1)作DF⊥AB,CH⊥AB垂足分别为F、G.
∵四边形ABCD是等腰梯形,
∴AF=BH,FH=DC=13.
在Rt△ADF中,tanA=
=
,
设DF=3x,则AF=4x,
由勾股定理AF2+DF2=AD2
∴(4x)2+(3x)2=102解得:x=2,
∴AF=BH=8.
∴AB=8+13+8=29.
(2)∵四边形ABCD是等腰梯形,
∴∠A=∠B.
当
=
时,△ADE∽△BCE,此时
=
=1,
∴BE=
AB=
.
当
=
时,△ADE∽△BEC,
此时BE(AB-BE)=AD•BC.
∴BE(29-BE)=10×10.
解得:BE=4或BE=25.
∴当BE=4或
或25,△AED与△BCE相似.
 解:(1)作DF⊥AB,CH⊥AB垂足分别为F、G.
解:(1)作DF⊥AB,CH⊥AB垂足分别为F、G.∵四边形ABCD是等腰梯形,
∴AF=BH,FH=DC=13.
在Rt△ADF中,tanA=
| DF |
| AF |
| 3 |
| 4 |
设DF=3x,则AF=4x,
由勾股定理AF2+DF2=AD2
∴(4x)2+(3x)2=102解得:x=2,
∴AF=BH=8.
∴AB=8+13+8=29.
(2)∵四边形ABCD是等腰梯形,
∴∠A=∠B.
当
| AD |
| BC |
| AE |
| BE |
| AD |
| BC |
| AE |
| BE |
∴BE=
| 1 |
| 2 |
| 29 |
| 2 |
当
| AD |
| BE |
| AE |
| BC |
此时BE(AB-BE)=AD•BC.
∴BE(29-BE)=10×10.
解得:BE=4或BE=25.
∴当BE=4或
| 29 |
| 2 |
点评:本题考查的等腰梯形的性质,相似三角形的判定定理以及勾股定理的理解及运用.

练习册系列答案
相关题目
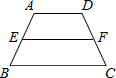 已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )
已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )| A、24 | B、22 | C、20 | D、16 |
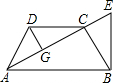 如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
 4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( )
4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( ) (2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )
(2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )