题目内容
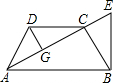如图，已知：在等腰梯形ABCD中，AB∥CD，AC⊥BC，DG⊥AC，过B作EB⊥AB，交AC的延长线于E．（1）求证：AD2=AC•CE；
（2）当BE=CD时，求证：△DCG≌△EBC．
分析：（1）因为等腰梯形ABCD，AB∥CD，所以∠DCA=∠CAB，又因为AC⊥BC，EB⊥AB，所以∠EBC=∠CAB，所以△ACB∽△BCE，得
=
，即BC2=AC•CE，又AD=BC，所以AD2=AC•CE
（2）由（1）可知∠EBC=∠BCG=∠CAB，又BE=CD，∠BCE=∠CGD，所以△DCG≌△EBC
| AC |
| BC |
| BC |
| CE |
（2）由（1）可知∠EBC=∠BCG=∠CAB，又BE=CD，∠BCE=∠CGD，所以△DCG≌△EBC
解答：证明：（1）∵等腰梯形ABCD，AB∥CD，
∴∠DCA=∠CAB．
∵AC⊥BC，EB⊥AB，
∴∠EBC=∠CAB，∠CEB=∠CBA．
∴△ACB∽△BCE．
∴
=
．
即BC2=AC•CE．
∵等腰梯形ABCD，
∴AD=BC．
∴AD2=AC•CE；
（2）∵由（1）知∠EBC=∠BCG=∠CAB，
∵BE=CD，∠BCE=∠CGD，
∴△DCG≌△EBC．
∴∠DCA=∠CAB．
∵AC⊥BC，EB⊥AB，
∴∠EBC=∠CAB，∠CEB=∠CBA．
∴△ACB∽△BCE．
∴
| AC |
| BC |
| BC |
| CE |
即BC2=AC•CE．
∵等腰梯形ABCD，
∴AD=BC．
∴AD2=AC•CE；
（2）∵由（1）知∠EBC=∠BCG=∠CAB，
∵BE=CD，∠BCE=∠CGD，
∴△DCG≌△EBC．
点评：本题中（1）主要考查了相似三角形的判定和等腰梯形的性质，（2）考查了全等三角形的判定
练习册系列答案
相关题目
