题目内容
求证：平行四边形的对角线互相平分（要求：根据题意先画出图形并写出已知、求证，再写出证明过程）．
已知：平行四边形ABCD的对角线AC，BD相交于点O，
求证：OA=OC，OB=OD
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠1=∠2，
在△AOD和△COB中，
∴△AOD≌△COB（AAS），
∴OA=OC，OB=OD．
练习册系列答案
相关题目
B、
C、
D、
．
，求∠ABF的度数；
，求⊙O的半径．
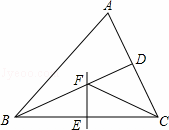
如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（ ）
|
| A． | 48° | B． | 36° | C． | 30° | D． | 24° |
﹣
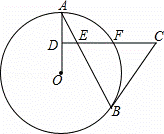
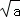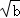）2≥0，所以a﹣2
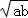+b≥0从而a+b≥2
当a=b时取等号）．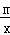
；（m＞0，x＞0，m为常数），由阅读1结论可知：x+
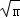，所以当x=
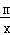的最小值为2
．
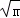，周长为2（x+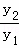
的最小值为 ；