题目内容
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB .
.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF ,求∠ABF的度数;
,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=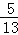 ,求⊙O的半径.
,求⊙O的半径.
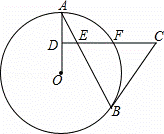
(1)证明:连接OB
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC
又∵CD⊥OA
∴∠A+∠AED=∠A+∠CEB=90°
∴∠OBA+∠ABC=90°
∴OB⊥BC
∴BC是⊙O的切线.
(2)解:如图1,连接OF,AF,BF,
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°
∴∠ABF= ∠AOF=30°;
∠AOF=30°;
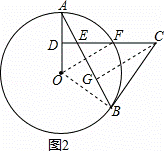
(3)解:如图2,过点C作CG⊥BE于G,
∵CE=CB,
∴EG= BE=5,
BE=5,
∵∠ADE=∠CGE=90°,∠AED=∠GEC,
∴∠GCE=∠A,
∴△ADE∽△CGE,
∴sin∠ECG=sin∠A= ,
,
在RtECG中,
∵CG= =12,
=12,
∵CD=15,CE=13,
∴DE=2,
∵△ADE∽△CGE,
∴ ,
,
∴AD=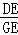 ,CG=
,CG= ,
,
∴⊙O的半径OA=2AD=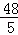 .
.


练习册系列答案
相关题目
2015年某中学举行的春季田径径运动会上,参加男子跳高的15名运动员的成绩如表所示:
| 成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
|
| A. | 1.70m,1.65m | B. | 1.70m,1.70m | C. | 1.65m,1.60m | D. | 3,4 |
 ;‚
;‚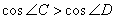 ;
;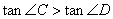 中,正确的结论为( )
中,正确的结论为( )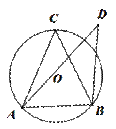
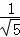 [
[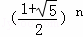 ﹣
﹣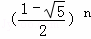 ]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
 中,最小的是
中,最小的是 
 +2x-3图像的顶点坐标是____________.
+2x-3图像的顶点坐标是____________.