题目内容
阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为(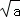 ﹣
﹣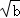 )2≥0,所以a﹣2
)2≥0,所以a﹣2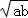 +b≥0从而a+b≥2
+b≥0从而a+b≥2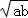 (
( 当a=b时取等号).
当a=b时取等号).
阅读2:若函数y=x+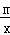 ;(m>0,x>0,m为常数),由阅读1结论可知:x+
;(m>0,x>0,m为常数),由阅读1结论可知:x+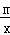 ≥2
≥2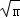 ,所以当x=
,所以当x=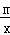 ,即x=
,即x=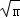 时,函数y=x+
时,函数y=x+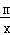 的最小值为2
的最小值为2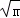 .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为2(x+
,周长为2(x+ ),求当x= 时,周长的最小值为 ;
),求当x= 时,周长的最小值为 ;
问题2:已知函数y1=x+1(x>﹣1)与函数y2=x2+2x+10(x>﹣1),
当x= 时,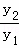 的最小值为 ;
的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
解:问题1:x= (x>0),解得x=2,
(x>0),解得x=2,
x=2时,x+ 有最小值为2×
有最小值为2× =4.
=4.
故当x=2时,周长的最小值为2×4=8.
问题2:∵函数y1=x+1(x>﹣1),函数y2=x2+2x+10(x>﹣1),
∴ =(x+1)+
=(x+1)+ ,
,
x+1= ,解得x=2,
,解得x=2,
x=2时,(x+1)+ 有最小值为2×
有最小值为2× =6.
=6.
问题3:设学校学生人数为x人,
则生均投入= =10+0.01x+
=10+0.01x+ =10+0.01(x+
=10+0.01(x+ ),
),
x= (x>0),解得x=700,
(x>0),解得x=700,
x=700时,x+ 有最小值为2×
有最小值为2× =1400,
=1400,
故当x=700时,生均投入的最小值为10+0.01×1400=24元.
答:当学校学生人数为700时,该校每天生均投入最低,最低费用是24元.
故答案为:2,8;2,6.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 =1
=1 =
=
 中,最小的是
中,最小的是  •
•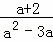 ﹣
﹣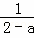 ,并求值,其中a与2、3构成△ABC的三边,且a为整数.
,并求值,其中a与2、3构成△ABC的三边,且a为整数.
 40000000毫升,将2540000000用科学记数法表示应为 。
40000000毫升,将2540000000用科学记数法表示应为 。 可售出100斤。通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤。为了保证每天至少售出260斤,张阿姨决定降价销售。
可售出100斤。通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤。为了保证每天至少售出260斤,张阿姨决定降价销售。