Question

有一张矩形纸片ABCD，已知AB=2cm，AD=4cm，上面有一个以AD为直径的半圆，如图甲，将它沿DE折叠，使A点落在BC上，如图乙，这时，半圆还露在外面的部分（阴影部分）的面积是（　　）

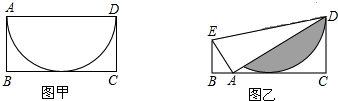
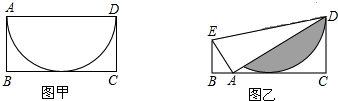
• A、(π-2

  3

  )cm2
• B、(

  1

  2

  π+

  3

  )cm2
• C、(

  4π

  3

  -

  3

  )cm2
• D、(

  2

  3

  π+

  3

  )cm2

Answer 1

考点：翻折变换（折叠问题）,扇形面积的计算

专题：

分析：如图，露在外面部分的面积可用扇形ODK与△ODK的面积差来求得．在Rt△ADC中，可根据AD即圆的直径和CD即圆的半径长，求出∠DAC的度数，进而得出∠ODA和∠ODK的度数，即可求得△ODK和扇形ODK的面积，由此可求得阴影部分的面积．

解答：解：∵以AD为直径的半圆，正好与对边BC相切，
∴AD=2CD，
∵∠C=90°，
∴∠DAC=30°，
∴∠ADC=60°，
∴∠DOK=120°，
∴扇形ODK的面积为

4

3

πcm²，
作OH⊥DK于H，
∵∠D=∠K=30°，OD=2cm，
∴OH=1cm，DH=

3

cm；
∴△ODK的面积为

3

cm²
∴半圆还露在外面的部分（阴影部分）的面积是（

4

3

π-

3

）cm²．
故选C．

点评：此题考查了折叠问题，解题时要注意找到对应的等量关系；还考查了圆的切线的性质，垂直于过切点的半径；还考查了直角三角形的性质，直角三角形中，如果有一条直角边是斜边的一半，那么这条直角边所对的角是30度．