题目内容
计算:
(1)(2a+3b)(3a-4b)
(2)(x+y+z)(x-y-z)
(1)(2a+3b)(3a-4b)
(2)(x+y+z)(x-y-z)
考点:平方差公式,完全平方公式
专题:计算题
分析:(1)原式利用多项式乘以多项式法则计算即可得到结果;
(2)原式利用平方差公式化简,再利用完全平方公式展开即可得到结果.
(2)原式利用平方差公式化简,再利用完全平方公式展开即可得到结果.
解答:解:(1)原式=6a2-8ab+9ab-12b2=6a2+ab-12b2;
(2)原式=x2-(y+z)2=x2-y2-2yz-z2.
(2)原式=x2-(y+z)2=x2-y2-2yz-z2.
点评:此题考查了平方差公式,以及完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
下列说法正确的是( )
| A、若ma=mb,则a=b | ||||
| B、若a2=b2,则a=b | ||||
| C、若a+m=b+m,则a=b | ||||
D、若x=y,则
|
△ABC中,各角的度数有下列关系:∠A=2∠B=3∠C,则△ABC一定是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
对一元二次方程x2+3x+3=0的根的情况叙述正确的是( )
| A、方程有一个实数根 |
| B、方程有两个不相等的实数根 |
| C、方程有两个相等的实数根 |
| D、方程没有实数根 |
 如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE=
如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE= 如图,∠1=∠2,∠3=100°,∠B=80°,那么DC∥EF,为什么?
如图,∠1=∠2,∠3=100°,∠B=80°,那么DC∥EF,为什么?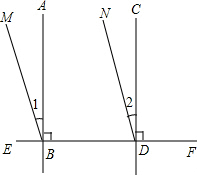 如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2
如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2