题目内容
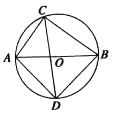
【题目】如图,△ABC是钝角三角形,![]() ,圆O是△ABC的外接圆,直径PQ恰好经过AB的中点M,PQ与BC的交点为D,
,圆O是△ABC的外接圆,直径PQ恰好经过AB的中点M,PQ与BC的交点为D,![]() ,l为过点C圆的切线,作
,l为过点C圆的切线,作![]() ,CF也为圆的直径.
,CF也为圆的直径.
(1)证明:![]() ;
;
(2)已知圆O的半径为3,求![]() 的值.
的值.
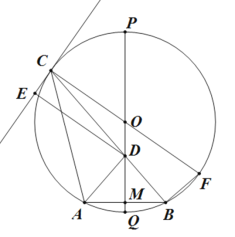
【答案】(1)见解析;(2)![]()
【解析】
(1)先证得CF//DE得到∠BCF=∠CDE,再证出∠CED=∠CBF=90°即可得到答案;
(2)连接AF,先证得△ADB为等腰直角三角形,得到∠ADB=∠ADC=90°,再求出AC=CF×sin45°=![]() ,即可得到答案.
,即可得到答案.
(1)∵CF为直径,l为切线,
∴![]() ,
,
又∵![]() ,
,
∴CF//DE,
∴∠BCF=∠CDE.
又∠CED=∠CBF=90°,
∴![]() ;
;
(2)连接AF,
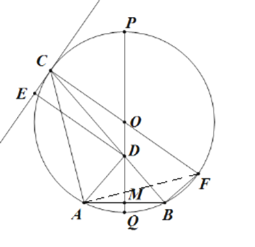
由题意得:∠CDP=∠BDM=45°,
∵M为弦AB的中点,
∴OM垂直平分线段AB,
∴∠ADM=∠BDM=45°,
∴△ADB为等腰直角三角形,
∴∠ADB=∠ADC=90°,
∴![]() ,
,
∵∠AFC=∠ABC=45°,
∴AC=CF×sin45°=![]() ,
,
∴![]() .
.

练习册系列答案
相关题目