Question

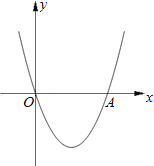
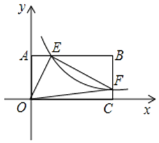
【题目】如图，将一矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的一个动点不与点A、B重合，过点E的反比例函数的图象与边BC交于点F

若的面积为，且，求k的值；

若，，反比例函数的图象与边AB、边BC交于点E和F，当沿EF折叠，点B恰好落在OC上，求k的值．

Answer 1

【答案】（1）2；（2）3.

【解析】

（1）设，则可得，，根据，可得，可得；

（2）过E作，垂足为D，沿EF折叠，点B恰好落在OC上的，根据点E、F在反比例函数的图象上，，，可得，，根据线段之间的等量关系可得：，，

根据，易证∽，可得，

根据可得出，在中，利用勾股定理可得出k的值.

解：设，则，，

点E在反比例函数上，

，

的面积为1，

，；

答：k的值为：2．

过E作，垂足为D，沿EF折叠，点B恰好落在OC上的，

，，点E、F在反比例函数的图象上，

，，

，，

，

，

,

,

，

∽,

可得：，

，

，

在中，由勾股定理得：

，解得：，

答：k的值为：3．