题目内容
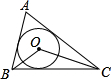如图所示，⊙O为△ABC的内切圆，∠ABC=80°，∠ACB=36°，则∠BOC=________°．
122
分析：由三角形内切圆定义可知：OB、OC是∠ABC、∠ACB的角平分线；再利用角平分线的定义可知∠OBC+∠OCB=
（∠ABC+∠ACB），代入数值即可求∠BOC=122°．
解答：∵OB、OC是∠ABC、∠ACB的角平分线，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=（80°+36°）=58°，
∴∠BOC=180°-58°=122°．
故答案为122．
点评：本题主要考查了三角形内切圆及三角形内角和定理，难度适中．
分析：由三角形内切圆定义可知：OB、OC是∠ABC、∠ACB的角平分线；再利用角平分线的定义可知∠OBC+∠OCB=
（∠ABC+∠ACB），代入数值即可求∠BOC=122°．解答：∵OB、OC是∠ABC、∠ACB的角平分线，
∴∠OBC+∠OCB=
（∠ABC+∠ACB）=（80°+36°）=58°，∴∠BOC=180°-58°=122°．
故答案为122．
点评：本题主要考查了三角形内切圆及三角形内角和定理，难度适中．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图所示，△ABC为等边三角形，BD为中线，延长BC至E，使DE=BD．求证：CE=
13、如图所示，△ABC为等边三角形，P是△ABC内任一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为12，则PD+PE+PF=
17、“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题，“今有圆材，埋壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言表述是：“如图所示，CD为⊙O的直径，CD⊥AB，垂足为E，CE=1寸，AB=1尺，求直径CD长是多少寸？”（注：1尺=10寸）
如图所示，O为直线AB上一点，OM平分∠AOC，ON平分∠BOC，则图中互余的角有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |
如图所示，P为正方形ABCD内一点，且PA：PB：PC=1：1：| 3 |
| A、120 | B、135 |
| C、150 | D、175 |