题目内容
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
(1)求证:∠PAC=∠B,且PA•BC=AB•CD;
(2)若PA=10,sinP=
,求PE的长.
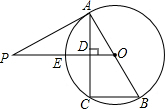
(1)求证:∠PAC=∠B,且PA•BC=AB•CD;
(2)若PA=10,sinP=
| 3 |
| 5 |

(1)证明:∵PA是⊙O的切线,AB是直径,
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B,
又∵OP⊥AC,
∴∠ADP=∠C=90°,
∴△PAD∽△ABC,
∴AP:AB=AD:BC,
∵在⊙O中,AD⊥OD,
∴AD=CD,
∴AP:AB=CD:BC,
∴PA•BC=AB•CD;
(2)方法一:
∵sinP=
,且AP=10,
∴
=
,
∴AD=6,
∴AC=2AD=12,
∵在Rt△ADP中,PD=
=8,
又∵△PAD∽△ABC,
∴AP:AB=PD:AC,
∴AB=
=15,
∴A0=OE=
,
在Rt△APO中,根据勾股定理得:OP=
=
,
∴PE=OP-OE=
-
=5.
方法二:
由sinP=
=
,设OA为3x,PO为5x,
由勾股定理得PA为4x,
∵PA=10,∴x=2.5,
∴OA=7.5,OP=12.5,
又∵OE=OA=7.5,
∴PE=OP-OE=5.
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B,
又∵OP⊥AC,
∴∠ADP=∠C=90°,
∴△PAD∽△ABC,
∴AP:AB=AD:BC,
∵在⊙O中,AD⊥OD,
∴AD=CD,
∴AP:AB=CD:BC,
∴PA•BC=AB•CD;
(2)方法一:
∵sinP=
| 3 |
| 5 |
∴
| AD |
| AP |
| 3 |
| 5 |
∴AD=6,
∴AC=2AD=12,
∵在Rt△ADP中,PD=
| AP2-AD2 |
又∵△PAD∽△ABC,
∴AP:AB=PD:AC,
∴AB=
| 10×12 |
| 8 |
∴A0=OE=
| 15 |
| 2 |
在Rt△APO中,根据勾股定理得:OP=
| AP2+OA2 |
| 25 |
| 2 |
∴PE=OP-OE=
| 25 |
| 2 |
| 15 |
| 2 |
方法二:
由sinP=
| 3 |
| 5 |
| AO |
| PO |
由勾股定理得PA为4x,
∵PA=10,∴x=2.5,
∴OA=7.5,OP=12.5,
又∵OE=OA=7.5,
∴PE=OP-OE=5.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目







