题目内容
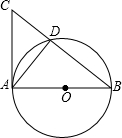
如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE．
（1）求证：DE是⊙O的切线；
（2）连接OE，若AB=4，AD=3，求OE的长．
（1）求证：DE是⊙O的切线；
（2）连接OE，若AB=4，AD=3，求OE的长．
（1）证明：连接OD，BD，
∵AB为圆O的直径，
∴∠ADB=90°，
在Rt△BDC中，E为斜边BC的中点，
∴CE=DE=BE=
BC，
∴∠C=∠CDE，
∵OA=OD，∴∠A=∠ADO，
∵∠ABC=90°，即∠C+∠A=90°，
∴∠ADO+∠CDE=90°，即∠ODE=90°，
∴DE⊥OD，又OD为圆的半径，
∴DE为圆O的切线；
（2）在Rt△ABD中，AB=4，AD=3，
根据勾股定理得：BD=
=
，
∵∠DAB=∠BAC，∠ADB=∠CBA=90°，
∴△ADB∽△ABC，
∴
=
，即
=
，
解得：BC=
，
在Rt△ABC中，根据勾股定理得：AC=
=
，
∵E为BC的中点，O为AB的中点，
∴OE为△ABC的中位线，
则OE=
AC=
．
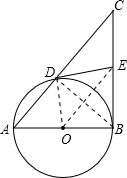
∵AB为圆O的直径，
∴∠ADB=90°，
在Rt△BDC中，E为斜边BC的中点，
∴CE=DE=BE=
| 1 |
| 2 |
∴∠C=∠CDE，
∵OA=OD，∴∠A=∠ADO，
∵∠ABC=90°，即∠C+∠A=90°，
∴∠ADO+∠CDE=90°，即∠ODE=90°，
∴DE⊥OD，又OD为圆的半径，
∴DE为圆O的切线；
（2）在Rt△ABD中，AB=4，AD=3，
根据勾股定理得：BD=
| AB2-AD2 |
| 7 |
∵∠DAB=∠BAC，∠ADB=∠CBA=90°，
∴△ADB∽△ABC，
∴
| AD |
| AB |
| DB |
| BC |
| 3 |
| 4 |
| ||
| BC |
解得：BC=
4
| ||
| 3 |
在Rt△ABC中，根据勾股定理得：AC=
| AB2+BC2 |
| 16 |
| 3 |
∵E为BC的中点，O为AB的中点，
∴OE为△ABC的中位线，
则OE=
| 1 |
| 2 |
| 8 |
| 3 |
练习册系列答案
相关题目
=∠BAP，AB=4，BP=x，CP=y，点C到MN的距离为线段CD的长．
P出发，点A以5cm/s的速度沿射线PM方向运动，点B以4cm/s的速度沿射线PN方向运动．设运动时间为ts．
