题目内容
6.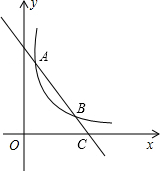 如图,直线y=-2x+4与双曲线y=$\frac{k}{x}$交于A、B两点,与x轴交于点C,若AB=2BC,则k=$\frac{3}{2}$.
如图,直线y=-2x+4与双曲线y=$\frac{k}{x}$交于A、B两点,与x轴交于点C,若AB=2BC,则k=$\frac{3}{2}$.
分析 直线y=-2x+4与双曲线y=$\frac{k}{x}$交于A、B两点,过A作AD⊥x轴于D,BE⊥x轴于E,直线y=-2x+4与x轴的交点为(2,0),根据相似三角形的性质列方程$\frac{2-\sqrt{4-2k}}{2+\sqrt{4-2k}}$=$\frac{1}{3}$,即可得到结果.
解答 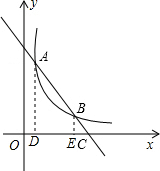 解:∵直线y=-2x+4与双曲线y=$\frac{k}{x}$交于A、B两点,
解:∵直线y=-2x+4与双曲线y=$\frac{k}{x}$交于A、B两点,
解$\left\{\begin{array}{l}{y=-2x+4}\\{y=\frac{k}{x}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{1}=\frac{2-\sqrt{4-2k}}{2}}\\{{y}_{1}=2+\sqrt{4-2k}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{1}=\frac{2+\sqrt{4-2k}}{2}}\\{{y}_{1}=2-\sqrt{4-2k}}\end{array}\right.$,
过A作AD⊥x轴于D,BE⊥x轴于E,
∵直线y=-2x+4与x轴的交点为(2,0),
∴OC=2,
∵AB=2BC,
∵△BCE∽△CAD,
∴$\frac{BE}{AD}=\frac{BC}{AC}$,
∴$\frac{2-\sqrt{4-2k}}{2+\sqrt{4-2k}}$=$\frac{1}{3}$,
∴k=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
17.想表示某人一天体温变化情况,应该利用( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上都可以 |
11.下列说法中错误的是( )
| A. | 若直线CD为线段AB的中垂线,则CA=CB,DA=DB | |
| B. | 若CA=CB,DA=DB,则直线CD垂直平分线段AB | |
| C. | 若CA=CB,则C在线段AB的垂直平分线上 | |
| D. | 若DA=DB,则经过点D的直线为线段AB的垂直平分线 |
18.已知x=$\frac{1}{y}$.x,y为非零有理数,那么(x-$\frac{1}{x}$)(y+$\frac{1}{y}$)等于( )
| A. | x2+y2 | B. | x2-y2 | C. | 2x | D. | 2y |
8.已知a,b,c是△ABC的三条边长,且a>b>c,若b=8,c=3,则a可能是( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
9.根据下列表格中的对应值,判断关于x的一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的一个根x1的范围正确的是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
| A. | -0.02<x1<0.03 | B. | 3.24<x1<3.25 | C. | -0.02≤x1≤0.03 | D. | 3.24≤x1≤3.25 |