题目内容
17．
如图，AO⊥OC于点O，DO⊥BO于点O，∠AOB：∠AOD=2：11，求∠AOB与∠BOC的度数．
分析 根据垂直的定义得到∠AOC=∠BOD=90°，根据余角的性质得到∠AOB=∠COD，求得∠AOB：∠BOC=2：7，根据∠AOB+∠BOC=90°，即可得到结论．
解答 解：∵AO⊥OC于点O，DO⊥BO于点O，
∴∠AOC=∠BOD=90°，
∴∠AOB=∠COD，
∵∠AOB：∠AOD=2：11，
∴∠AOB：∠BOC=2：7，
∵∠AOB+∠BOC=90°，
∴∠AOB=20°，∠BOC=70°．
点评 本题考查了垂线的性质，能够根据已知条件列方程解答是解题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7．十一黄金周期间，某风景区在7天假期中每天观光人数变化如表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
（1）若9月30日的游客人数为4.2千人，写出这七天实际游客人数，试说明这七天内游客人数最多的是哪天？最少的是哪天？它们相差多少千人？
（2）以9月30日的游客人数为0点，用折线统计图表示这7天的游客人数情况．
| 日期 | 人数变化/千人 |
| 1号 | +1.2 |
| 2号 | +0.7 |
| 3号 | +0.3 |
| 4号 | -0.2 |
| 5号 | -0.4 |
| 6号 | +0.1 |
| 7号 | -1.3 |
（2）以9月30日的游客人数为0点，用折线统计图表示这7天的游客人数情况．
由若干个相同的小立方体组成一个几何体，从其上面看到的平面图形如图所示，其中的数字表示在该位置上的小立方体的层数．请分别画出从正面和左面看这个几何体得到的平面图形．
用圆规、直尺作图，不写作法，但要保留作图痕迹．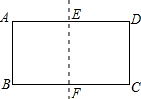
如图，将矩形ABCD沿两条长边中点的连线EF对折，如果矩形BFEA与矩形ABCD相似，求AB：AD的值．