题目内容
18.抛物线y=2x2-7x+3与x轴交于A,B两点,顶点为C,则△ABC的面积为$\frac{125}{32}$.分析 首先令y=2x2-7x+3=0求出点A和点B的坐标,然后求出顶点C的坐标,最后利用三角形的面积公式求出答案.
解答 解:∵抛物线y=2x2-7x+3与x轴交于A,B两点,
∴方程2x2-7x+3=0的解为x1=$\frac{1}{2}$,x2=3,
∴A,B两点的坐标分别为A($\frac{1}{2}$,0),B(3,0),
又∵抛物线y=2x2-7x+3可化为:y=2(x-$\frac{7}{4}$)2-$\frac{25}{8}$,
∴C点坐标为C($\frac{7}{4}$,-$\frac{25}{8}$),
∴S△ABC=$\frac{1}{2}$AB•|yc|=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{25}{8}$=$\frac{125}{32}$.
故答案为:$\frac{125}{32}$.
点评 本题主要考查了抛物线与x轴的交点的知识,解答本题的关键是根据顶点坐标式求出顶点C的坐标,此题难度一般.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
13.两个数的和是负数,而积是正数,那么这两个数( )
| A. | 都是正数 | B. | 都是负数 | C. | 一正一负 | D. | 同号 |
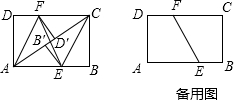
 如图所示,已知AB∥CD,分别探索下列两个图形中∠P,∠A,∠C的关系,请你写出来,并证明你的结论.
如图所示,已知AB∥CD,分别探索下列两个图形中∠P,∠A,∠C的关系,请你写出来,并证明你的结论.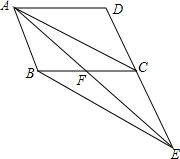 如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于F.
如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于F.