题目内容
已知函数y=y1+y2,其中y1与-2x成正比列,y2与x2成反比例,且x=1时,y=-5,x=-1时,y=7,求出y与x的函数关系及x=2时,y的值.
考点:待定系数法求反比例函数解析式
专题:计算题
分析:根据正比例函数和反比例函数的定义,设y1=-2ax,y2=
,则y=-2ax+
,再把两组对应值代入得到关于a、b的方程组,解方程组求出a、b即可得到y与x的函数关系式,然后计算自变量为2的函数值即可.
| b |
| x2 |
| b |
| x2 |
解答:解:设y1=-2ax,y2=
,则y=-2ax+
,
把x=1时,y=-5,x=-1时,y=7分别代入得
,解得
,
所以y与x的函数关系式为y=-6x+
,
当x=2时,y=-6x+
=-12+
=-
.
| b |
| x2 |
| b |
| x2 |
把x=1时,y=-5,x=-1时,y=7分别代入得
|
|
所以y与x的函数关系式为y=-6x+
| 1 |
| x2 |
当x=2时,y=-6x+
| 1 |
| x2 |
| 1 |
| 4 |
| 47 |
| 4 |
点评:本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法种数共有( )
| A、6种 | B、5种 | C、4种 | D、3种 |
点P(-2,-1)关于y轴对称的点的坐标是( )
| A、(-2,-1) |
| B、(1,-2) |
| C、(2,-1) |
| D、(-1,-2) |
 某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由.
某小区的一所健身中心的平面图如图所示,活动区是面积为200m2的钜形,其长为20m,餐饮区是一个半圆形,面积为πm2,休息区是一个三角形,试判断此三角形的形状,并说明理由. 如图,已知点C、D在线段AB上,若AC=
如图,已知点C、D在线段AB上,若AC=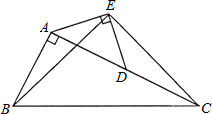 如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.