��Ŀ����
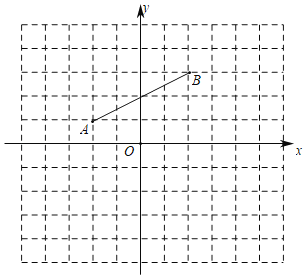
����Ŀ��ij��˾����һ�ֳɱ�����Ϊ50Ԫ/�����²�Ʒ���涨����ʱ���۵��۲����ڳɱ����ۣ��ֲ�����80Ԫ/�������������飬����������y�����������۵���x��Ԫ/�����ɽ��ƿ���һ�κ���y��kx+b�Ĺ�ϵ����ͼ��ʾ��
��I������ͼ����һ�κ���y��kx+b�Ľ���ʽ����д���Ա���x��ȡֵ��Χ��
���ù�˾Ҫ��ÿ������������Ӧ�����۵��۶�Ϊ���٣��������ֵΪ���٣�

���𰸡���1��y=��x+100��50��x��80������2�����۵��۶�Ϊ75Ԫ/�����������Ϊ625Ԫ��
��������
��1���������⣬���ô���ϵ������һ�κ����Ľ���ʽ��������2����ÿ���õ�����ΪWԪ����������W�����۵���x�Ķ��κ���ģ�ͣ����ݶ��κ��������ʼ��������
�⣺��1���ɺ�����ͼ��ã�![]() ��
��
��ã�![]() ��
��
������y=��x+100��50��x��80����
��2����ÿ���õ�����ΪWԪ��
����1���ã�W=��x��50��y=��x��50������x+100��=��x2+150x��5000=����x��75��2+625��
����1��0��
�൱x=75ʱ��W���=625���ù�˾Ҫ��������������Ӧ�����۵���Ϊ75Ԫ/�����������Ϊ625Ԫ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ�˱���������ij�������ۺ�����ָ�Ӳ���������![]() ��
��![]() �����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����
�����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����![]() �ͺŵ���ˮ�����豸��̨������75��Ԫ����
�ͺŵ���ˮ�����豸��̨������75��Ԫ����![]() �ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
�ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
��ˮ�����豸 |
|
|
�۸���Ԫ/̨�� |
|
|
�´�����ˮ������/̨�� | 220 | 180 |
��1����![]() ��ֵ��
��ֵ��
��2���������ʽ����ƣ�ָ�Ӳ����ڹ�����ˮ�����豸���ʽ���156��Ԫ�����ж����ֹ����������ÿ����ദ����ˮ���Ķ�����