Question

【题目】如图，在平面直角坐标系中，线段AB的两个端点坐标分别为（﹣2，1）和（2，3）．

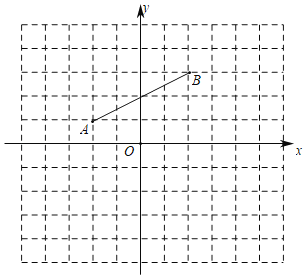
（1）在图中分别画出线段AB关于x轴的对称线段A1B1，并写出A1、B1的坐标．

（2）在x轴上找一点C，使AC+BC的值最小，在图中作出点C，并直接写出点C的坐标．

Answer 1

【答案】（1）图见解析，A1的坐标为（﹣2，﹣1）、B1的坐标为（2，﹣3）；（2）图见解析，点C坐标为（﹣1，0）

【解析】

（1）分别作出点A、B关于x轴的对称点，再连接即可得；

（2）连接，与x轴的交点即为所求；再根据点坐标、以及等腰直角三角形的判定与性质可求出OC的长，从而可得点C坐标．

（1）如图所示，即为所求：

由点关于x轴对称的坐标变换规律：横坐标不变，纵坐标变为相反数

的坐标为，的坐标为；

（2）由轴对称的性质得：

则

要使的值最小，只需的值最小

由两点之间线段最短得：的值最小值为

因此，连接，与x轴的交点即为所求的点C，如图所示：

则是等腰直角三角形，

是等腰直角三角形

故点C坐标为