题目内容
 已知在△ABC中,点D、E、F分别为BC、AD、CE的中点,且S△ABC=6cm2,则S△BEF的值为________cm2.
已知在△ABC中,点D、E、F分别为BC、AD、CE的中点,且S△ABC=6cm2,则S△BEF的值为________cm2.
1.5
分析:由于D、E、F分别为BC、AD、CE的中点,可判断出AD、BE、CE、BF为△ABC、△ABD、△ACD、△BEC的中线,根据中线的性质可知将相应三角形分成面积相等的两部分,据此即可解答.
解答:∵由于D、E、F分别为BC、AD、CE的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
S△BEC= S△ABC=3(cm2).
S△ABC=3(cm2).
S△BEF= S△BEC=
S△BEC= ×3=1.5(cm2).
×3=1.5(cm2).
故答案为:1.5.
点评:此题考查了三角形的面积,根据三角形中线将三角形的面积分成相等的两部分解答.
分析:由于D、E、F分别为BC、AD、CE的中点,可判断出AD、BE、CE、BF为△ABC、△ABD、△ACD、△BEC的中线,根据中线的性质可知将相应三角形分成面积相等的两部分,据此即可解答.
解答:∵由于D、E、F分别为BC、AD、CE的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
S△BEC=
 S△ABC=3(cm2).
S△ABC=3(cm2).S△BEF=
 S△BEC=
S△BEC= ×3=1.5(cm2).
×3=1.5(cm2).故答案为:1.5.
点评:此题考查了三角形的面积,根据三角形中线将三角形的面积分成相等的两部分解答.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
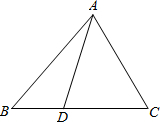 (2012•上海模拟)如图,已知在△ABC中,点D在边BC上,且BD:DC=1:2.如果
(2012•上海模拟)如图,已知在△ABC中,点D在边BC上,且BD:DC=1:2.如果 (2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
(2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( ) 如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.
如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.