题目内容
20.先化简再求值:($\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$,其中x=-$\frac{1}{2}$.分析 根据分式混合运算的法则先把括号里面的式子通分,把分子相加减,再算除法,最后把x=-$\frac{1}{2}$的值代入进行计算即可.
解答 解:原式=[$\frac{2x(x+1)}{(x+1)(x-1)}$-$\frac{x(x-1)}{(x-1)^{2}}$]•$\frac{x+1}{x}$
=[$\frac{2x}{x-1}$-$\frac{x}{x-1}$]•$\frac{x+1}{x}$
=$\frac{x}{x-1}$•$\frac{x+1}{x}$
=$\frac{x+1}{x-1}$,
当x=-$\frac{1}{2}$时,原式=$\frac{-\frac{1}{2}+1}{-\frac{1}{2}-1}$=-$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
11.在-22、(-2)2、-(-2)、-|-2|中,负数的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15. 如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )
如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )
 如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )
如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
5.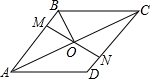 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |