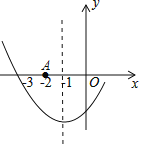题目内容
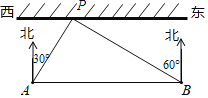
【题目】为了保证端午节龙舟赛在我市侨港海域顺利举办,某部门工作人员乘快艇到侨港海域考察水情,以每秒11米的速度沿平行于岸边的赛道AB由西向东行驶,在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
【答案】建筑物P到赛道AB的距离为110![]() 米.
米.
【解析】
作PC⊥AB于C,构造出Rt△PAC与Rt△PBC,求出AB的长度,利用特殊角的三角函数值求解.
过P点作PC⊥AB于C,由题意可知:∠PAC=60°,∠PBC=30°,

在Rt△PAC中,![]() =tan∠PAC,
=tan∠PAC,
∴AC=![]() PC,
PC,
在Rt△PBC中,![]() =tan∠PBC,
=tan∠PBC,
∴BC=![]() PC,
PC,
∵AB=AC+BC=![]() PC+
PC+![]() PC=11×40,
PC=11×40,
∴PC=110![]() ,
,
答:建筑物P到赛道AB的距离为110![]() 米.
米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
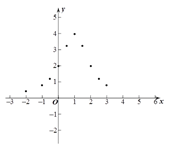
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .