题目内容
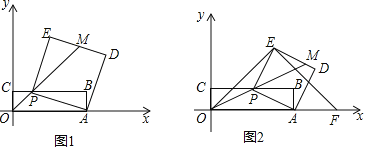
【题目】已知:如图1,矩形OABC的两个顶点A,C分别在x轴,y轴上,点B的坐标是(8,2),点P是边BC上的一个动点,连接AP,以AP为一边朝点B方向作正方形PADE,连接OP并延长与DE交于点M,设CP=a(a>0).
(1)请用含a的代数式表示点P,E的坐标.
(2)连接OE,并把OE绕点E逆时针方向旋转90°得EF.如图2,若点F恰好落在x轴的正半轴上,求a与![]() 的值.
的值.
(3)①如图1,当点M为DE的中点时,求a的值.
②在①的前提下,并且当a>4时,OP的延长线上存在点Q,使得EQ+![]() PQ有最小值,请直接写出EQ+
PQ有最小值,请直接写出EQ+![]() PQ的最小值.
PQ的最小值.
【答案】(1)P(a,2);E(a+2,10﹣a);(2)a=4,![]() =3;(3)①a=2或6;②
=3;(3)①a=2或6;②![]() .
.
【解析】
(1)如图1中,作![]() 于N只要证明
于N只要证明![]() ,即可解决问题;
,即可解决问题;
(2)利用等腰直角三角形的性质,根据点E的坐标构建方程求出a,再构建一次函数求出点M坐标,即可解决问题;
(3)①求出点M坐标,根据![]() =
=![]() ,构建方程即可;
,构建方程即可;
②如图4中,将![]() 绕点P顺时针旋转
绕点P顺时针旋转![]() 得到
得到![]() ,则
,则![]() 是等腰直角三角形.可得
是等腰直角三角形.可得![]() 的中点
的中点![]() ,
,![]() ,作
,作![]() ,则
,则![]() ,推出
,推出![]() ,可得当E、Q、R共线时,
,可得当E、Q、R共线时,![]() 的值最小,求出点R坐标即可解决问题;
的值最小,求出点R坐标即可解决问题;
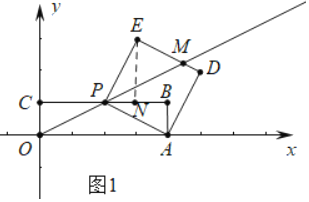
解:(1)如图1中,作![]() 于N.
于N.
∵B![]() ,
,
∴BC=8,![]() ,∵
,∵![]() ,
,
∴![]()
∵四边形OABC是矩形,四边形ADEP是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
(2)如图2中,
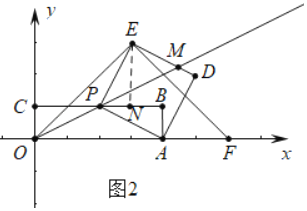
由题意:△EOF是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴a=4,![]() ,
,
∴直线OP的解析式为![]() ,直线DE的解析式为
,直线DE的解析式为![]() ,
,
由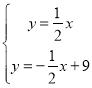 ,解得
,解得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)①如图3中,作![]() 于K.
于K.
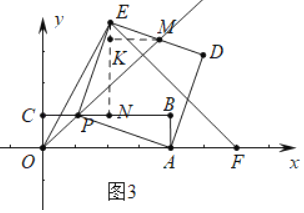
由![]() ,可得,
,可得,![]() ,
,
∴EK=1,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴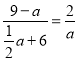 ,
,
整理得:![]() ,
,
解得![]() 或6.
或6.
②如图4中,将![]() 绕点P顺时针旋转
绕点P顺时针旋转![]() 得到
得到![]() ,则
,则![]() 是等腰直角三角形.
是等腰直角三角形.
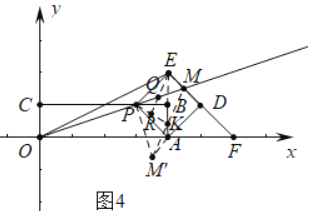
由题意a=6,![]() ,
,
∴![]() 的中点
的中点![]() ,
,
∵![]() ,
,
∴![]() ,作
,作![]() ,则
,则![]() ,
,
∴![]() ,
,
∴当E、Q、R共线时,![]() 的值最小,
的值最小,
∵直线PR的解析式为![]() ,
,
∵![]() ,
,
∴直线ER的解析式为![]() ,
,
由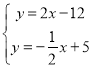 ,解得
,解得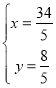 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.