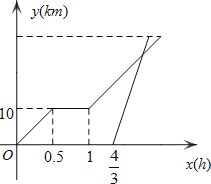
题目内容
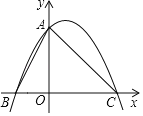
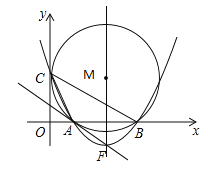
【题目】如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A、B两点．
（1）则点A、B、C的坐标分别是A（__，__），B（__，__），C（__，__）；
（2）设经过A、B两点的抛物线解析式为
，它的顶点为F，求证：直线FA与⊙M相切；
（3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形．如果存在，请求出点P的坐标；如果不存在，请说明理由．
【答案】（1）A（2，0），B（8，0），C（0，4）；（2）证明见试题解析；（3）P（5，4），或（5，
），或（5，
）．
【解析】
（1）连接MC，则MC垂直于y轴，MA=MC=5，MD=4，由勾股定理可计算AD和DB；
（2）把A、或B或C的坐标代入y=
，确定二次函数表达式y=
，连接MA，根据勾股定理计算AF，由勾股定理逆定理判断MA⊥AF，从而说明FA是切线；
（3）设P（x，4），当C为顶点时，在Rt△CMP1中用x表示CP1，根据
列方程求解；当B为顶点时，在Rt△BDP2中用x表示CP2，根据
列方程求解；当P是顶点时，易知P和M重合．
解：（1）连接MC，则MC垂直于y轴，MA=MC=5，MD=4，在Rt△AMD中，AD=
=3，同理在Rt△BMD中，BD=3
∴A（2，0），B（8，0），C（0，4）；
（2）把A（2，0）y=，解得k=-
∴y=，∴F（5，-）
连接MA，则MF=4+=
，AF=
=
∴
∴MA⊥AF
∴FA与⊙M相切；
（3）设P（x，4），
当C为顶点时，在Rt△CMP1中，
∴
，x=
点P在x轴上方，故x=，所以（，4）；
当B为顶点时，在Rt△BDP2中，
∴
，x=
，点P在x轴上方
故x=
，所以（，4）；
当P是顶点时，P和M重合，P3（5，4）．
综上当P（，4）、（，4）或（5，4）时△PBC是等腰三角形．
