题目内容
17. 如图,在△ABC中,DE∥BC,已知CD=1,BC=1.8,DE=1.5,求AD的长.
如图,在△ABC中,DE∥BC,已知CD=1,BC=1.8,DE=1.5,求AD的长.
分析 由在△ABC中,DE∥BC,可得△ADE∽△ACB,又由CD=1,BC=1.8,DE=1.5,根据相似三角形的对应边成比例,即可求得AD的长.
解答 解:∵在△ABC中,DE∥BC,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}=\frac{DE}{BC}$,
∵CD=1,BC=1.8,DE=1.5,
∴$\frac{AD}{AD+1}=\frac{1.5}{1.8}$,
解得:AD=5.
点评 此题考查了相似三角形的判定与性质.注意相似三角形的对应边成比例.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
8.一元二次方程x2+5=-4x的一次项的系数是( )
| A. | 4 | B. | -4 | C. | 1 | D. | 5 |
9.若x,y满足|x+2|+(y-2)2=0,则($\frac{x}{y}$)2009的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
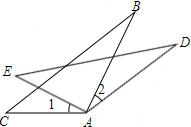 如图,AC=AE,AB=AD,∠1=∠2,求证:∠B=∠D.
如图,AC=AE,AB=AD,∠1=∠2,求证:∠B=∠D.