题目内容
己知实数x满足x+
=3,又
=
,则m=( )
| 1 |
| x |
| x3+mx2+x |
| x4+2mx2+1 |
| 1 |
| 3 |
分析:先把x+
=3方程两边都乘以x,求出x2+1=3x,两边都平方,然后再乘以x2,求出x4+1=7x2,再整体代入分式约分后得到关于m的方程,求解即可.
| 1 |
| x |
解答:解:∵x+
=3,
∴x2+1=3x,x2+2+
=9,
∴x4+1=7x2,
∴
=
=
=
=
,
∴9+3m=7+2m,
解得m=-2.
故选A.
| 1 |
| x |
∴x2+1=3x,x2+2+
| 1 |
| x2 |
∴x4+1=7x2,
∴
| x3+mx2+x |
| x4+2mx2+1 |
| x(x2+1)+mx2 |
| 7x2+2mx2 |
| 3x2+mx2 |
| 7x2+2mx2 |
| 3+m |
| 7+2m |
| 1 |
| 3 |
∴9+3m=7+2m,
解得m=-2.
故选A.
点评:本题考查了分式的化简求值,根据完全平方公式把已知条件整理出所求分式中的分子、分母中的部分多项式的形式是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 =3,又
=3,又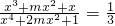 ,则m=
,则m=