题目内容
12.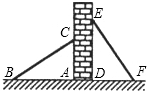 如图,有两个长度相等(BC=EF)的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,求证:∠ABC+∠DFE=90°.
如图,有两个长度相等(BC=EF)的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,求证:∠ABC+∠DFE=90°.
分析 先根据BC=EF,AC=DF判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质可知,∠ABC=∠DEF,再由直角三角形的两锐角互余即可解答.
解答 证明:在Rt△ABC和Rt△DEF中,
∵$\left\{\begin{array}{l}{BC=EF}\\{AC=DF}\end{array}\right.$,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
点评 本题考查的是全等三角形的判定及性质、直角三角形的性质,正确得出Rt△ABC≌Rt△DEF是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列说法,正确的是( )
| A. | -52 与(-5)2相等 | |
| B. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| C. | -a2表示一个负数 | |
| D. | 两个有理数的差不一定小于被减数 |

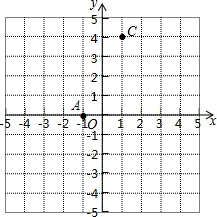 如图,A(-1,0),C(1,4),点B在x轴上,且AB=4.
如图,A(-1,0),C(1,4),点B在x轴上,且AB=4. 如图,已知A(2,3),B(1,1),C(4,1),M(6,3).
如图,已知A(2,3),B(1,1),C(4,1),M(6,3).