题目内容
1.能将代数式配成完全平方式.(1)x2-4x=(x-2)2+(-4)
(2)x2-6x+9=(x-3)2
(3)x2+px+$\frac{{p}^{2}}{4}$=(x+$\frac{p}{2}$)2.
分析 把两项的乘方分别算出来,再算出两项的乘积,再乘以2,然后把这个数放在两数的乘方的中间,这个数以前一个数间的符号随原式中间的符号,完全平方和公式就用+,完全平方差公式就用-,后边的符号都用+.依此即可求解.
解答 解:(1)x2-4x=(x-2)2+(-4)
(2)x2-6x+9=( x-3)2
(3)x2+px+$\frac{{p}^{2}}{4}$=( x+$\frac{p}{2}$)2.
故答案为:-2,(-4);9,x-3; $\frac{{p}^{2}}{4}$,x+$\frac{p}{2}$.
点评 此题考查了完全平方式,完全平方式分两种,一种是完全平方和公式,就是两个整式的和括号外的平方.另一种是完全平方差公式,就是两个整式的差括号外的平方.算时有一个口诀“首末两项算平方,首末项乘积的2倍中间放,符号随中央”.

练习册系列答案
相关题目
9.把分式$\frac{3x}{x+y}$中的x,y都扩大两倍,那么分式的值( )
| A. | 不变 | B. | 扩大两倍 | C. | 缩小两倍 | D. | 无法确定 |
6.数据2,3,8,5,7的极差为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,在?ABCD中,∠B=46°,则∠D=46°.
如图,在?ABCD中,∠B=46°,则∠D=46°. 如图,经过坐标原点O的直线AB与双曲线y=$\frac{-3}{x}$相交于A,B两点,BC⊥x轴于点C,连结AC,则△AOC的面积为$\frac{3}{2}$.
如图,经过坐标原点O的直线AB与双曲线y=$\frac{-3}{x}$相交于A,B两点,BC⊥x轴于点C,连结AC,则△AOC的面积为$\frac{3}{2}$. 如图,在?ABCD中,E、F分别在AB,CD边上,且AE=CF.
如图,在?ABCD中,E、F分别在AB,CD边上,且AE=CF.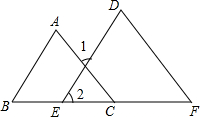 如图填空:
如图填空: 如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区(用阴影画),并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是30m,求小华家到公路的距离.
如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区(用阴影画),并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是30m,求小华家到公路的距离. 已知:如图,O点在△ABC内部,连AO、BO、CO,A′、B′、C′分别在AO、BO、CO上,且AB∥A′B′、BC∥B′C′.图中△OAC与△OA′C′相似吗?为什么?
已知:如图,O点在△ABC内部,连AO、BO、CO,A′、B′、C′分别在AO、BO、CO上,且AB∥A′B′、BC∥B′C′.图中△OAC与△OA′C′相似吗?为什么?