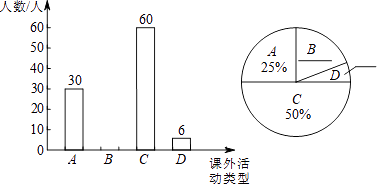
ĢāÄæÄŚČŻ
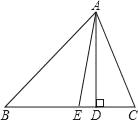
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻACB=90”ć£¬Å×ĪļĻßy=©x2+bx+c¾¹żA£¬BĮ½µć£¬ĘäÖŠµćA£¬CµÄ×ų±ź·Ö±šĪŖ£Ø1£¬0£©£¬£Ø©4£¬0£©£¬Å×ĪļĻߵĶ„µćĪŖµćD£®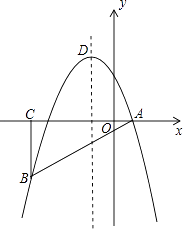
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćEŹĒÖ±½ĒČż½ĒŠĪABCŠ±±ßABÉĻµÄŅ»øö¶Æµć£Ø²»ÓėA£¬BÖŲŗĻ£©£¬¹żµćE×÷xÖįµÄ“¹Ļߣ¬½»Å×ĪļĻßÓŚµćF£¬µ±Ļ߶ĪFEµÄ³¤¶Č×ī“óŹ±£¬ĒóµćEµÄ×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Å×ĪļĻßÉĻŹĒ·ń“ęŌŚŅ»µćP£¬Ź¹”÷PEFŹĒŅŌEFĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬Ēó³öĖłÓŠµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗ”ßA£¬CµÄ×ų±ź·Ö±šĪŖ£Ø1£¬0£©£¬£Ø©4£¬0£©£¬
”ąAC=5£®
”ß”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻC=90”ć£¬
”ąBC=AC=5£®
”ąB£Ø©4£¬©5£©£®
½«µćAŗĶµćBµÄ×ų±ź“śČėµĆ£ŗ ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ ![]() £¬
£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=©x2©2x+3£®
£Ø2£©½ā£ŗČēĶ¼1ĖłŹ¾£ŗ
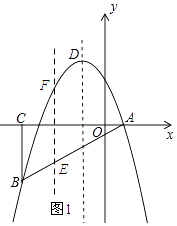
ÉčÖ±ĻßABµÄ½āĪöŹ½ĪŖy=kx+b£¬½«µćAŗĶµćBµÄ×ų±ź“śČėµĆ£ŗ ![]() £¬½āµĆ£ŗk=1£¬b=©1£®
£¬½āµĆ£ŗk=1£¬b=©1£®
ĖłŅŌÖ±ĻßABµÄ½āĪöŹ½ĪŖy=x©1£®
ÉčµćEµÄ×ų±źĪŖ£Øt£¬t©1£©£¬ŌņµćFµÄ×ų±źĪŖ£Øt£¬©t2©2t+3£©£®
”ąEF=©t2©2t+3©£Øt©1£©=©t2©3t+4=£Øt+ ![]() £©2+
£©2+ ![]() £®
£®
”ąµ±t=© ![]() Ź±£¬FEČ”×ī“óÖµ
Ź±£¬FEČ”×ī“óÖµ ![]() £¬“ĖŹ±£¬µćEµÄ×ų±źĪŖ£Ø©
£¬“ĖŹ±£¬µćEµÄ×ų±źĪŖ£Ø© ![]() £¬©
£¬© ![]() £©£®
£©£®
£Ø3£©½ā£ŗ“ęŌŚµćP£¬ÄÜŹ¹”÷PEFŹĒŅŌEFĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£®
ĄķÓÉ£ŗČēĶ¼ĖłŹ¾£ŗ¹żµćF×÷Ö±Ļßa”ĶEF£¬½»Å×ĪļĻßÓŚµćP£¬¹żµćE×÷Ö±Ļßb”ĶEF£¬½»Å×ĪļĻßP”䔢P”壮
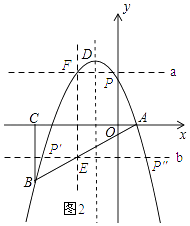
ÓÉ£Ø2£©æÉÖŖµćEµÄ×ų±źĪŖ£Øt£¬t©1£©£¬ŌņµćFµÄ×ų±źĪŖ£Øt£¬©t2©2t+3£©£¬t=© ![]() £¬
£¬
”ąµćE£Ø© ![]() £¬©
£¬© ![]() £©”¢F£Ø©
£©”¢F£Ø© ![]() £¬
£¬ ![]() £©£®
£©£®
¢Łµ±©t2©2t+3= ![]() Ź±£¬½āµĆ£ŗx=©
Ź±£¬½āµĆ£ŗx=© ![]() »ņx=©
»ņx=© ![]() £ØÉįČ„£©£®
£ØÉįČ„£©£®
”ąµćPµÄ×ų±źĪŖ£Ø© ![]() £¬
£¬ ![]() £©£®
£©£®
¢Śµ±©t2©2t+3=© ![]() Ź±£¬½āµĆ£ŗx=©1+
Ź±£¬½āµĆ£ŗx=©1+ ![]() »ņx=©1©
»ņx=©1© ![]() £®
£®
”ąµćP”ä£Ø©1© ![]() £¬©
£¬© ![]() £©£¬P”å£Ø©1+
£©£¬P”å£Ø©1+ ![]() £¬©
£¬© ![]() £©£®
£©£®
×ŪÉĻĖłŹö£¬µćPµÄ×ų±źĪŖ£Ø© ![]() £¬
£¬ ![]() £©»ņ£Ø©1©
£©»ņ£Ø©1© ![]() £¬©
£¬© ![]() £©»ņP”å£Ø©1+
£©»ņP”å£Ø©1+ ![]() £¬©
£¬© ![]() £©£®
£©£®
”¾½āĪö”æ£Ø1£©ŅŖĒó½āĪöŹ½¹Ų¼üŌŚÓŚĒóBµć×ų±ź£¬ÓÉ”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻC=90”ć£¬BC=AC=5£®æÉĒó³öB£Ø©4£¬©5£©£¬°ŃA”¢B×ų±ź“śČė½āĪöŹ½¼“æÉ£»£Ø2£©Ēó×īÖµĪŹĢāæɻƹéĪŖŗÆŹż×īÖµĪŹĢā£¬Ņņ“ĖŠė¹¹½ØŅŌEµćŗį×ų±źtĪŖ×Ō±äĮ攢EF³¤¶ČĪŖŅņ±äĮæµÄŗÆŹż£¬ÓĆtµÄ“śŹżŹ½±ķŹ¾EF£¬EFŹĒŹśÖ±Ļ߶Ī£¬Ę䳤¶ČæÉÓĆÉĻ¶Ėµćׯ×ų±ź¼õĻĀ¶Ėµćׯ×ų±ź£¬¹¹½ØŗÆŹżŗó£¬ČōŹĒ¶ž“ĪŗÆŹżæÉÓĆÅä·½·ØĒó³ö×īÖµ£»£Ø3£©ŅŌEFĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪæÉ·ÖĪŖĮ½Ąą£ŗŅŌEĪŖÖ±½Ē¶„µć£»ŅŌFĪŖÖ±½Ē¶„µć£»Ņņ“ĖŠė¹żE”¢F·Ö±š×÷EFµÄ“¹Ļß ÓėÅ×ĪļĻߵĽ»µć¾ĶŹĒPµć.