题目内容
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB'C'.

(1)在正方形网格中,画出△AB'C';
(2)计算线段AB在旋转到AB'的过程中所扫过区域的面积.(结果保留 )
)
(1)作图见试题解析;(2) .
.
【解析】
试题分析:(1)根据旋转的性质作出图形;
(2)线段AB在旋转到 的过程中所扫过区域是一个扇形,且它的圆心角为90°,半径为5.由扇形的面积公式可以求出结果.
的过程中所扫过区域是一个扇形,且它的圆心角为90°,半径为5.由扇形的面积公式可以求出结果.
试题解析:(1)画图如图.

(2)由图可知△ABC是直角三角形,AC=4,BC=3,所以AB=5.线段AB在旋转到 的过程中所扫过区域是一个扇形,且它的圆心角为90°,半径为5.∴
的过程中所扫过区域是一个扇形,且它的圆心角为90°,半径为5.∴  .所以线段AB在旋转到
.所以线段AB在旋转到 的过程中所扫过区域的面积为
的过程中所扫过区域的面积为 .
.
考点:1.作图-旋转变换;2.扇形面积的计算.

练习册系列答案
相关题目
 h.如果设骑自行车的速度为
h.如果设骑自行车的速度为 km/h,则由题意可列方程为 .
km/h,则由题意可列方程为 .
 的顶点坐标是( )
的顶点坐标是( )
 的值.
的值.
 向右平移3个单位,再向下平移2个单位,得到抛物线( )
向右平移3个单位,再向下平移2个单位,得到抛物线( ) B.
B.
 D.
D.

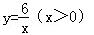 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
 的x的取值范围;
的x的取值范围;