Question

7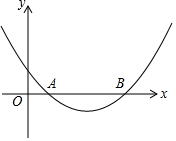．如图，抛物线y=ax²+bx+1过A（1，0）、B，（5，0）两点．
（1）求：抛物线的函数表达式；
（2）求：抛物线与y轴的交点C的坐标及其对称轴
（3）若抛物线对称轴上有一点P，使△COA∽△APB，求点P的坐标．

Answer 1

分析 （1）把A、B两点坐标代入，可求得a、b的值，可求得抛物线的函数表达式；
（2）根据（1）中所求抛物线的解析式可求得C点的坐标，及对称轴；
（3）由A、C点的坐标可判定△COA为等腰直角三角形，若△COA∽△APB，可知△APB为等腰直角三角形，利用直角三角形的性质可求得P到x轴的距离，可求得P点坐标．

解答 解：
（1）∵抛物线y=ax²+bx+1过A（1，0）、B，（5，0）两点，
∴$\left\{\begin{array}{l}{a+b+1=0}\\{25a+5b+1=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=\frac{1}{5}}\\{b=-\frac{6}{5}}\end{array}\right.$，
∴抛物线的函数表达式为y=$\frac{1}{5}$x²-$\frac{6}{5}$x+1；

（2）在y=$\frac{1}{5}$x²-$\frac{6}{5}$x+1中，令x=0可得y=1，
∴C点坐标为（0，1），
又y=$\frac{1}{5}$x²-$\frac{6}{5}$x+1=$\frac{1}{5}$（x-3）²-$\frac{4}{5}$，
∴抛物线对称轴为直线x=3；

（3）∵A（1，0），C（0，1），
∴OA=OC=1，
∴△COA为等腰直角三角形，且∠COA=90°，
∵△COA∽△APB，
∴△APB为等腰直角三角形，∠APB=90°，
∵P在抛物线对称轴上，
∴P到AB的距离=$\frac{1}{2}$AB=$\frac{1}{2}$×（5-1）=2，
∴P点坐标为（3，2）或（3，-2）．

点评 本题为二次函数的综合应用，涉及待定系数法、二次函数的性质、相似三角形的性质、等腰直角三角形的性质等知识．在（1）中注意待定系数法的应用步骤，在（2）中，也可以直接利用对称轴公式求解，在（3）中由直角三角形的性质求得P点到x轴的距离是解题的关键．本题考查知识点较多，综合性较强，但难度不大，较易得分．