题目内容
在△ABC中,AD是∠BAC的平分线.(1)如图①,求证:
| S△ABD |
| S△ACD |
| AB |
| AC |
(2)如图②,若BD=CD,求证:AB=AC;
(3)如图③,若AB=5,AC=4,BC=6.求BD的长.

分析:(1)作DE⊥AB于E,DF⊥AC于F,由角平分线的性质可知,DE=DF,再由三角形的面积公式求解即可;
(2)根据BD=CD,可知S△ABD=S△ACD,根据(1)的结论即可得到
=1,即AB=AC;
(3)过A作AE⊥BC,垂足为E,由三角形的面积公式可得出
=
,再由(1)的结论即可求出BD的长.
(2)根据BD=CD,可知S△ABD=S△ACD,根据(1)的结论即可得到
| AB |
| AC |
(3)过A作AE⊥BC,垂足为E,由三角形的面积公式可得出
| S△ABD |
| S△ACD |
| BD |
| DC |
解答:
解:(1)如图①,证明:作DE⊥AB于E,DF⊥AC于F,∵AD是∠BAC的平分线,
∴DE=DF
∴
=
=
;
(2)∵BD=CD,∴S△ABD=S△ACD
由(1)的结论
=
,
∴
=1,
∴AB=AC;
(3)如图③,过A作AE⊥BC,垂足为E,
∵S△ABD=
BD•AE,S△ACD=
DC•AE,
∴
=
由(1)的结论
=
,
∴
=
=
,
∴BD=
,DC=
.

解:(1)如图①,证明:作DE⊥AB于E,DF⊥AC于F,∵AD是∠BAC的平分线,
∴DE=DF
∴
| S△ABD |
| S△ACD |
| ||
|
| AB |
| AC |
(2)∵BD=CD,∴S△ABD=S△ACD
由(1)的结论
| S△ABD |
| S△ACD |
| AB |
| AC |
∴
| AB |
| AC |
∴AB=AC;
(3)如图③,过A作AE⊥BC,垂足为E,
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| S△ABD |
| S△ACD |
| BD |
| DC |
由(1)的结论
| S△ABD |
| S△ACD |
| AB |
| AC |
∴
| BD |
| DC |
| AB |
| AC |
| 5 |
| 4 |
∴BD=
| 10 |
| 3 |
| 8 |
| 3 |
点评:本题考查的是角平分线的性质及三角形的面积公式,由角平分线的性质及三角形的面积公式作出辅助线是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.
在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.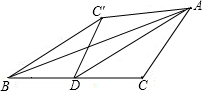 如图,在△ABC中,AD是BC上的中线,BC=4,∠ADC=30°,把△ADC沿AD所在直线翻折后点C落在点C′的位置,那么点D到直线BC′的距离是
如图,在△ABC中,AD是BC上的中线,BC=4,∠ADC=30°,把△ADC沿AD所在直线翻折后点C落在点C′的位置,那么点D到直线BC′的距离是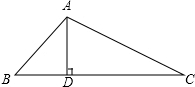
 (2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F.
(2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F. 如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF.
如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF.